Résolution d'un problème d'arithmétique et division euclidienne
-
MMeide dernière édition par Hind
Bonjour à tous,
Je suis nouveau et je me suis inscrit sur ce forum car je n'arrive pas à finir mon Dm de Spé Math dont l'énoncer est la suivante :
Citation
1- Soit n un entier strictement supérieur à 1. On suppose que l'écriture décimale de n² se termine par le chiffre 6.
a- Quel est nécessairement le chiffre des unités de n ? Le démontrer
b- Justifier qu'il existe un entier k tel que n s'écrive sous la forme 10k+4 ou 10k-4
c- Démontrer alors que le chiffre des unités de n² est 6 si est seulement si, n²+4 est un multiple de 20
2- Soit n>1. On note :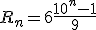
a- Justifier que pour tout n supérieur ou égal à 2, Rn est un entier
b- Quel est le reste de la division de Rn par 20
c- En déduire qu'aucun des Rn n'est un carréeEt voici mes réponses :
1-a-On écris n=10d+u
n²= (10d+u)² = 100d² + 20du + u²
le chiffre des unités de n² est le même que celui de u² donc le chiffre des unités de n² est 6 car u²=6
Et donc le chiffre des unités de n est : u=4 ou 6 car 4²=16 et 6²=36b- Un nombre ayant pour unité 4 s'écrit : 10k+4 ou 10k-6
Un nombre ayant pour unité 6 s'écrit : 10k+6 ou 10k-4
donc il existe un entier k tel que n s'écrive sous la forme 10k+4 ou 10k-4c- n²+4 = 100k²+16 + 4 = 100k²+20 donc n²+4 multiple de 20 pour n=10k+4
n²+4 = 100k²+36+4 = 100k²+ 40 = 100k²+ 2x20 donc n²+4 multiple de 20 si n=10k-4
Donc le chiffre des unités de n² est 6 si est seulement si, n²+4 est un multiple de 202-a-
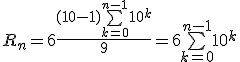
Donc Rn est un entier .b-
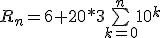
Donc le reste de la division euclidienne de Rn par 20 est 6
( Je ne suis pas sur du tout pour cette réponse )c- Je ne vois pas comment en déduire cela grâce aux questions précédentes ....
Voila, si vous pouviez confirmer mes réponses et m'aider à le terminer se serait super

Merci d'avanceMeide
-
Mmathtous dernière édition par
Bonjour,
Citation
le chiffre des unités de n² est le même que celui de u² donc le chiffre des unités de n² est 6 car u²=6
u² ne peut pas être égal à 6 qui n'est pas un carré.
On a n² ≡ 6 modulo 10 , donc u² ≡ 6 modulo 10
Envisage toutes les possibilités pour u.
-
MMeide dernière édition par
Et bien u=6 ou u=4, je ne vois pas ce qui peut y avoir comme autre solution ...
-
Mmathtous dernière édition par
Certes, mais il faut dire que ce sont les seules possibilités car les autres (u=0,u=1,u=2,u=3,u=5,u=7,u=8,u=9) ne donnent pas le chiffre souhaité.
Question b :
Citation
Un nombre ayant pour unité 4 s'écrit : 10k+4 ou 10k-6"ou 10k-6" est inutile.
Citation
Un nombre ayant pour unité 6 s'écrit : 10k+6 ou 10k-4Ici, oui, mais il vaut mieux écrire 10k+6 ou 10k'-4 ( ce n'est pas le même k ).2-a : oui
2-b : le raisonnement est juste mais il me semble qu'il y ait un décalage d'indice dans le mauvais sens : n'est-ce pas jusqu'à n-2 ( et non jusqu'à n )?J'avais oublié 1-c : c'est faux : (10k+4)² ≠ 100k²+16 !!
-
MMeide dernière édition par
Je me corrige :
Meide1-a-On écris n=10d+u
n²= (10d+u)² = 100d² + 20du + u²
n²=6[10] donc u²=6[10]
Tableau de congruence modulo 10 avec u et u²
Et donc le chiffre des unités de n est : u=4 ou 6 car 4²=16 et 6²=36b- Un nombre ayant pour unité 4 s'écrit : 10k+4
Un nombre ayant pour unité 6 s'écrit : 10k+6 ou 10k'-4
donc il existe un entier k tel que n s'écrive sous la forme 10k+4 ou 10k-4c- n²+4 = 100k²+80k+16+4= 5x20k²+4x20k+20= 20(5k²+4k+1) donc n²+4 multiple de 20 pour n=10k+4
n²+4 = 100k²-80k+16+4 = 5x20k²-4x20k+20=20(5k²-4k+1) donc n²+4 multiple de 20 si n=10k-4
Donc le chiffre des unités de n² est 6 si est seulement si, n²+4 est un multiple de 202-a-
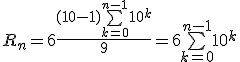
Donc Rn est un entier .b- $r_n = 6 + 20*3 \bigsum_{k=0}^{n-2} 10^k$
Donc le reste de la division euclidienne de Rn par 20 est 6Voila j'espère que c'est bon, je me suis effectivement trompé de sens pour l'indice de la 2-b mais même avec sa je ne vois pas pourquoi Rn ne pourrait être un carré ... Parce que si il est au carrée R2R_2R2=66
En tous cas, merci pour ton aide

-
Mmathtous dernière édition par
Citation
n²+4 = 100k²-80+16+4-80k, ça ne change rien au raisonnement.
2-c :
Effectivement, R2 n'est pas un carré. Mais tu dois démontrer que jamais Rn n'est un carré.
Facile : si Rn était un carré, Rn +4 serait un multiple de 20 car son chiffre des unités est 6 ( question 1-c ).
Donc Rn serait congru à 16 modulo 20.
Mais il est congru à 6 modulo 20, d'où la réponse.
Remarque : tu comprends maintenant pourquoi il a fallu voir ce que ça donnait modulo 20, car seulement modulo 10, il n'y aurait pas de contradiction.
-
MMeide dernière édition par
D'accord, j'ai corrigé pour le -80k
Je rédige la 2-c :Si Rn est un carré alors Rn+4 est un multiple de 20 car son chiffre des unités est 6
Il faut donc que Rn soit congrue a 16 modulo 20
Or Rn est congrue a 6 modulo 20
Donc Rn+4 n'est pas un multiple de 20 et donc son chiffre des unités de peut pas être 6 => Contradiction : Aucun des Rn ne peut être un carréeJe m'interroge sur ce raisonnement, ne devrais je pas plutôt écrire RRR_n2^22 +4 ?
-
MMeide dernière édition par
J'ai finalement compris, enfaite ce que l'énoncé voulait dire c'est x²=Rn
Je te remercie pour ton aide
-
Mmathtous dernière édition par
De rien.