Etudier une fonction exponentielle
-
CCess dernière édition par Hind
Bonjour,
J'ai un problème avec le développement de la question a) je pense,
Parce que toutes les autres propositions y font référence... Il y a peu de chance je pense pour que une seule proposition soit bonne si on a de précisé qu'il peut y avoir plusieurs réponses possibles, et qu'il faut justifier nos réponses...Voici le sujet:
On considère la fonction g:x→e3x−32e2x+1\frac{e^{3x}-3}{2e^{2x}+1}2e2x+1e3x−3
a) Que je pense fausse vu que mon développement ne donne pas pareil...
Pour tout x réel, g(x)=ex×(1−3e−3x2+e−2xe^{x}\times (\frac{1-3e^{-3x}}{2+e^{-2x}}ex×(2+e−2x1−3e−3x
b) limx→+∞ g(x)=+∞\lim_{x\rightarrow +\infty\ }g(x) =+\inftylimx→+∞ g(x)=+∞ et limx→−∞g(x)=0\lim_{x\rightarrow -\infty } g(x)=0limx→−∞g(x)=0
c) la fonction g(x) est dérivable sur R et :
g′(x)=2e2x(ex+1)(2e2x−2ex+3)(2+e−2x)2g'(x)=\frac{2e^{2x}(e^{x}+1)(2e^{2x}-2e^{x}+3)}{(2+e^{-2x})^{2}}g′(x)=(2+e−2x)22e2x(ex+1)(2e2x−2ex+3)
Et là on voit que le terme utilisé pour le (v)² du dénominateur de g'(x) est celui de la fonction g(x) proposée dans la a)... Ca peut paraitre confus... Je réexpliquerai si besoin.d)La quantité 2e2x(ex+1)(2e2x−2ex+3)2e^{2x}(e^{x}+1)(2e^{2x}-2e^{x}+3)2e2x(ex+1)(2e2x−2ex+3) est du signe (ex+1)(e^{x}+1)(ex+1) car pour tout réel x, 2e2x(ex+1)(2e2x−2ex+3)2e^{2x}(e^{x}+1)(2e^{2x}-2e^{x}+3)2e2x(ex+1)(2e2x−2ex+3) > 0.
La fonction g est donc décroissante sur ]-∞;-1] et croissante sur [-1;+∞[.La encore pour que ce soit vrai il faudrait que la a) soit vraie....
Mon développement de a) me donne ex−3e−2x2ex+e−x\frac{e^{x}-3e^{-2x}}{2e^{x}+e^{-x}}2ex+e−xex−3e−2x
Donc pas du tout la même chose. Si vous pouviez m'aider à trouver mes erreurs dans mon développement ou autre, ce serait bien, pour que je puisse faire correctement le reste de l'exercice...
Merci d'avance.
-
Zauctore dernière édition par

Bonsoir
c'est un vrai/faux cet exo ?
a) est juste.
b) la limite en -∞ est fausse.
ce que tu dis de ton développement pour a) en bas de post montre une erreur grossière ; la relation (élémentaire) à utiliser est
a×bc=a×bca\times \frac bc = \frac{a \times b}ca×cb=ca×b
où le dénominateur n'est pas concerné par la multiplication par "a".
-
CCess dernière édition par
Ah oui merci... en effet... La a) est donc juste.
-
CCess dernière édition par
Pourquoi pour la b) en -∞ c'est faux?? On prend la limite de exe^xex vu qu'elle est de plus haut degré non??
Et sa limite en -∞ est bien de 0.... Je ne comprend pas.
Je fais la c) en attendant.
-
CCess dernière édition par
J'ai essayé la c), j'ai du me tromper... Parce que ENCORE je n'arrive pas au bon résultat...
Ma dérivée est de : 2ex+e−x−3e−4x+e−x(2+e−2x)2\frac{2e^{x}+e^{-x}-3e^{-4x}+e^{-x}}{(2+e^{-2x})^{2}}(2+e−2x)22ex+e−x−3e−4x+e−x
Soit de : e−x(2e2x+1−3e−3x+1)(2+e−2x)2\frac{e^{-x}(2e^{2x}+1-3e^{-3x}+1)}{(2+e^{-2x})^{2}}(2+e−2x)2e−x(2e2x+1−3e−3x+1)Bref je ne vois pas où est mon erreur j'ai beau chercher... Non je vois pas.
Bon je n'ai pas donné tout mon développement, mais en gros j'ai calculé la dérivée de la partie fraction de l'équation obtenue grâce à la question a), et ensuite cela m'a permis de calculer la dérivée de exe^xex fois cette partie fractionnelle...Ah et OUI c'est un vrai faux, un QCM plus précisément.
-
Zauctore dernière édition par lisaportail

Bonjour
tu travailles tard dis donc.
voyons cette limite en -∞ :
tu sais que pour la fonction exponentielle limx→−∞ex=0\lim_{x \to -\infty} \text{e}^x = 0limx→−∞ex=0, donc limx→−∞e2x=0\lim_{x \to -\infty} \text{e}^{2x} = 0limx→−∞e2x=0 et limx→−∞e3x=0\lim_{x \to -\infty} \text{e}^{3x} = 0limx→−∞e3x=0.
ainsi, limx→−∞e3x−32e2x+1=−31\lim_{x \to -\infty} \frac{\text{e}^{3x}-3}{2\text{e}^{2x}+1} = \frac{-3}{1}limx→−∞2e2x+1e3x−3=1−3 et non 0.
Confirmation :
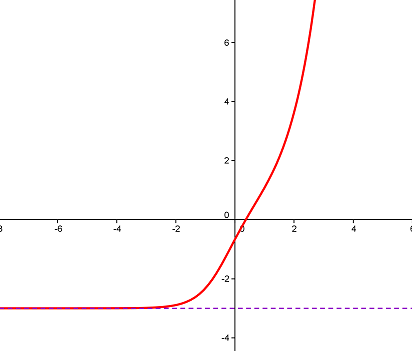
(s'il en était besoin)Je regarde le reste plus tard ^^
-
CCess dernière édition par
Bonjour, oui quand je suis dans mes maths, je lache pas facilement ^^.
Et toi tu travaille bien tôt!!Ah oui..je vois pour la limite en -∞. Non la confirmation n'est pas nécessaire. Enfin ça me permet de bien situer la chose, c'est déjà ça.
Par contre j'ai fait le calcul de la limite en +∞, si tu veux bien vérifier que c'est juste...
g(x)=e3x(1−3e3x)2e2x(1+12e2x)g(x)=\frac{e^{3x}(1-\frac{3}{e^{3x}})}{2e^{2x}(1+\frac{1}{2e^{2x}})}g(x)=2e2x(1+2e2x1)e3x(1−e3x3)
Donc, limx→+∞(1−3e3x)=1\lim_{x\rightarrow +\infty } (1-\frac{3}{e^{3x}})=1limx→+∞(1−e3x3)=1
Et limx→+∞(1+12e2x)=1\lim_{x\rightarrow +\infty }(1+\frac{1}{2e^{2x}})=1limx→+∞(1+2e2x1)=1Ainsi limx→+∞g(x)=limx→+∞e3x2e2x\lim_{x\rightarrow +\infty }g(x)= \lim_{x\rightarrow +\infty }\frac{e^{3x}}{2e^{2x}}limx→+∞g(x)=limx→+∞2e2xe3x
Or limx→+∞ex=limx→+∞e2x=limx→+∞e3x=+∞\lim_{x\rightarrow +\infty } e^{x}=\lim_{x\rightarrow +\infty }e^{2x}=\lim_{x\rightarrow +\infty }e^{3x}=+\inftylimx→+∞ex=limx→+∞e2x=limx→+∞e3x=+∞
e3x2e2x=e2x(ex)2ex(ex)=e2x2ex=ex(ex)2∗(ex)=ex2\frac{e^{3x}}{2e^{2x}}=\frac{e^{2x}(e^{x})}{2e^{x}(e^{x})}=\frac{e^{2x}}{2e^{x}}=\frac{e^{x}(e^{x})}{2*(e^{x})}=\frac{e^{x}}{2}2e2xe3x=2ex(ex)e2x(ex)=2exe2x=2∗(ex)ex(ex)=2ex
Donc limx→+∞g(x)=limx→+∞ex2=+∞\lim_{x\rightarrow +\infty } g(x) = \lim_{x\rightarrow +\infty } \frac{e^{x}}{2} = +\inftylimx→+∞g(x)=limx→+∞2ex=+∞
Est-ce juste??
-
CCess dernière édition par
Pour la dernière question je bloque.. J'ai essayer de résoudre l'inégalité. Mais je ne suis pas sure que ce soit la bonne méthode à faire... Merci pour ton aide.
-
CCess dernière édition par
Je suis encore dessus mais je n'y arrive pas... Chui devenue vraiment nulle en maths... C'est.. pitoyable.
-
CCess dernière édition par
Je dois rendre mon DM demain si tu pouvais me répondre pour ces deux dernières questions avant 22 heures ce serait génial. Sinon tant pis j'y arrive vraiment pas, je le rendrai pas complet..
Merci en tout cas pour toute l'aide que tu m'as déjà apporté!!