Probabilité aléatoire
-
Ddut dernière édition par mtschoon
Bonsoir,
Est-il possible d'avoir des piste sur cet énoncé:Merci beaucoup
Observation de la modération
Le demandeur a visiblement effacé son énoncé (par souci de discrétion...). Fort dommage pour ceux qui consultent, car les explications données perdent de leur valeur...!
S'il y a récidive, cette attitude ne sera pas tolérée.
-
mtschoon dernière édition par mtschoon

Dut bonjour,
Si ce "oui" te gène, je pense qu'il faut comprendre que lorsque Bob dit "oui" c'est qu'il affirme que "Alice lui a donné la plus grande des deux valeurs, c'est à dire A2"
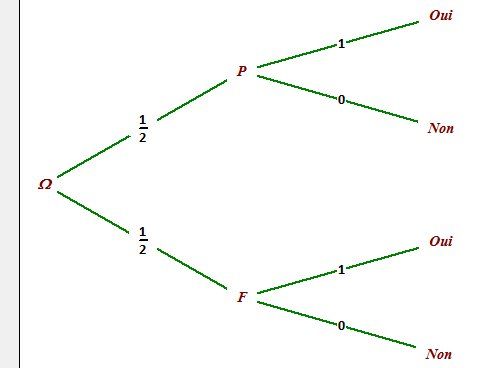
Eventuellement, je te mets un arbre pour clarifier la situation
(Les deux sous-branches "Non" avec probabilité nulle ne sont pas indispensables)
-
Ddut dernière édition par
Bonsoir Mtschoon,
Merci pour votre réponse c'est effectivement beaucoup plus clair.
Néanmoins je n'arrive pas à me décider sur la probabilité que Bob gagne. J'hésite entre 0,25 et 0,5. Je pencherai plus vers 0,5 mais la phrase "Bob va devoir deviner A2" me bloque. Je me demande s'il ne faut pas regarder que dans une seule branche (A2) 'OUI'.
-
mtschoon dernière édition par mtschoon

Bonsoir Dut,
Effectivement, il faut regarder sur la seule branche P(A2) suivie de Oui.
Probabilité 12×1\dfrac{1}{2}\times 121×1=12\dfrac{1}{2}21
La probabilité de gagner de Bob est donc 12\dfrac{1}{2}21
Bien sûr, cela sous-entend de mettre les probabilités sur l'arbre et ensuite d'utiliser le principe :
La somme des probabilités des branches issues d'un même sommet donne 1.
La probabilité d'un chemin est le produit des probabilités des branches qui le composent.
-
Ddut dernière édition par
Bonjour Mtschoon, j'ai identifié mon problème. Je ne comprends pas pourquoi on a comme proba pour "oui" 1 et pour "non" 0.
Vu que Alice à 1/2 chance de donner un bob la valeur de A2 Bob a une chance 1/2 de répondre "oui" ou "non".Je me pose la question aussi que si P vaut 0,5 les branches d'après (soit "oui " et "non") leur somme doivent faire 0,5 (soit la proba de P) ou 1. Dit différent "oui"=0,25 ou 0,5 et "non" =0,25 ou 0,5
Merci
-
mtschoon dernière édition par mtschoon

Ce que tu indiques n'est pas clair...
Ce que fait Alice est indépendant de ce que fait Bob.
Alice tire à Pile ou Face avec une pièce non biaisée donc probabilité 1/2 de tirer Pile et 1/2 de tirer Face
(Donc, elle a "50 chances sur 100" de tirer P et "50 chances sur 100" de tirer F)
Tu peux ainsi vérifier que la somme des probabilités de ces 2 branches issues d'un même sommet donne 1
1/2+1/2=1Quelque soit la pièce tirée par Alice, Bob répond Oui.
Donc, il a" 100 chances sur 100" de répondre Oui c'est à dire probabilité égale à 1 et a" 0 chance sur 100" de répondre Non c'est à dire probabilité égale à 0
Tu peux ainsi vérifier encore que la somme des probabilités de ces 2 branches issues d'un même sommet donne 1
1+0=1Ensuite, tu appliques la méthode :
La probabilité d'un chemin est le produit des probabilités des branches qui le composent.Le chemin satisfaisant est P suivi de Oui :
12×1=12\dfrac{1}{2}\times 1=\dfrac{1}{2}21×1=21
-
Ddut dernière édition par
Merci Mtschoon c'est limpide maintenant.
Mais pour rebondir sur votre explication il est demandé plus loin dans l'énoncé une autre stratégie permettant à Bob de tomber juste strictement plus d’une fois sur deux.
Je pense que c'est possible mais je ne vois pas comment car si on continu de regarder la branche A2 mais si on baisse la probabilité valant "1" alors obligatoirement les chances de Paul vont baisser
-
mtschoon dernière édition par mtschoon

Dut, bonjour,
C'est bien si la première partie est maintenant limpide pour toi.
Je regarde ta dernière question.Il faut interpréter le mieux possible ...
Tu as indiqué au début :
" Bob doit deviner si Alice lui a indiqué la plus grande des deux valeurs ou pas."
Je pense (?) qu'il faut comprendre que Bob a "juste" dans deux cas :
En répondant Oui lorsque Alice tire la face (A2) ou bien en répondant Non lorsque Alice tire la Face (A1) .
Dans ta première question, vu que Bob disait toujours Oui, le second cas ne pouvait pas arriver (la probabilité qu'il dise Non était nulle)Il faut donc maintenant qu'il "panache" les Oui et les Non
Je te mets un exemple :
Bob affirme Oui avec la probabilité 0.8 lorsqu'Alice tire P(A2) et Non avec la probabilité 0.5 lorsqu'Alice tire F(A1)
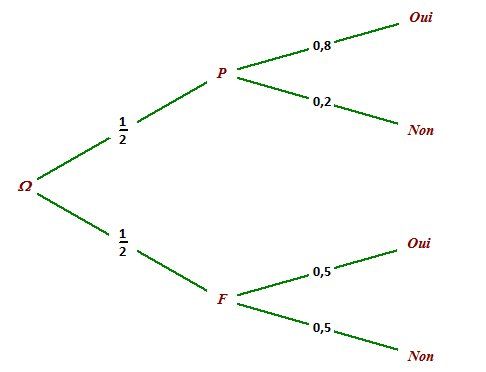
Tu as deux branches à regarder !
la branche P(A2) suivie de Oui et la branche F(A1) suivie de NonProbabilité : (12×0.8)+(12×0.5)=0.4+0.25=0.65\biggl(\dfrac{1}{2}\times 0.8\biggl) +\biggl(\dfrac{1}{2}\times 0.5\biggl)=0.4+0.25=0.65(21×0.8)+(21×0.5)=0.4+0.25=0.65
On a bien 0.65>0.50.65 \gt 0.50.65>0.5Il faut, je suppose, donner un résultat général.
Bob affirme Oui avec la probabilité a lorsqu'Alice tire P(A2) et Non avec la probabilité b lorsqu'Alice tire F(A1)Probabilité : (12×a)+(12×b)=12(a+b)\biggl(\dfrac{1}{2}\times a\biggl) +\biggl(\dfrac{1}{2}\times b\biggl)=\dfrac{1}{2}(a+b)(21×a)+(21×b)=21(a+b)
12(a+b)>0.5\dfrac{1}{2}(a+b)\gt 0.5 21(a+b)>0.5 <=> a+b>120.5a+b \gt \dfrac{\dfrac{1}{2}}{0.5}a+b>0.521 <=> a+b>0.50.5a+b \gt \dfrac{0.5}{0.5}a+b>0.50.5 <=> a+b>1\boxed{a+b\gt 1}a+b>1
a+b>1a+b \gt 1a+b>1 est la condition à réaliser pour que Bob puisse avoir donné une réponse "juste" avec une probabilité strictement supérieure à 0.5.
(dans l'exemple proposé a=0.8, b=0.5 et a+b=1.3 donc a+b> 1)
-
Ddut dernière édition par
Bonsoir Mtschoon, Merci pour votre explication
Je ne pensais pas regarder la branche "non" mais c'est vrai que c'est "logique" car on alterne les "oui" et "non".Si maintenant je veux calculer le gain il suffit que je multiplie les valeurs choisies avec la probabilité obtenue via l'arbre?
-
mtschoon dernière édition par mtschoon

Dut, bonjour,
De quel gain s'agit -il ?
Peut-être que tu parles seulement de la probabilité pour que Bob réponde de façon exacte ( c'est à dire "gagne") , via l'arbre réalisé dans mon topic précédent
Les calculs sont faits et la probabilité est de 65%, et de façon générale c'est 12(a+b)\dfrac{1}{2}(a+b)21(a+b)
Si c'est ça (?) , vu la fin de ta phrase, je pense que tu as bien compris le principe de l'arbre.
-
Ddut dernière édition par
Bonjour Mtschoon,
La question précise est:
Élaborez une autre stratégie permettant à Bob de tomber juste strictement plus d’une fois sur deux.Si vous avez trouvé :
Évaluez le gain de cette stratégie lorsque Alice choisit A1= 0.4 et A2= 0.6. Évaluez le gain de cette stratégie lorsque Alice tire ses deux nombres uniformément dans l’intervalle[0,1].
-
mtschoon dernière édition par mtschoon

Dut, bonjour,
Merci d'avoir indiquer clairement ta question.
Mais les termes employés ne sont pas précisés...Je t'indique mon interprétation personnelle.
Cette question est une généralisation de la question précédente.Il ne s'agit plus de lancer une pièce non biaisée pour obtenir l'équiprobabilité : p(P)=1/2 c'est à dire p(A2)=1/2 et p(F)=1/2 c'est à dire p(A1)=1/2
Il n'y a plus d'équiprobabilité pour le choix d'Alice et tu utilises donc : p(A2)=0.6 et P(A1)=0.4
Tu fais l'arbre probabiliste avec ces nouvelles données.
Avec la méthode d'utilisation de l'arbre (déjà vue), tu calcules la probabilité pour que Bob réponde de façon exacte en fonction de a et b, puis l'inéquation qui doit être réalisée pour que cette probabilité soit strictement supérieure à 1/2.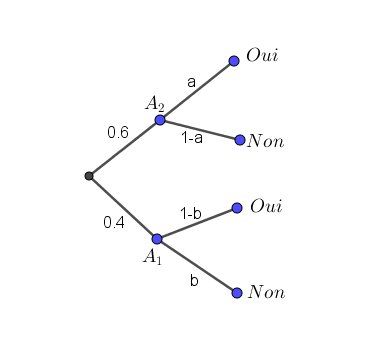
Généralisation :
x et y étant deux nombres quelconques de [0,1] tels que x+y=1
Soit P(A2)=x et p(A1)=y=1-x
Tu refais l'arbre avec ces données , ce qui te permet d'expliciter la probabilité pour que Bob réponde de façon exacte en fonction de x,a,b, puis l'inéquation qui doit être réalisée pour que cette probabilité soit strictement supérieure à 1/2.Personnellement, c'est tout ce que je peux dire avec cet énoncé...
Bon travail !
Remarque : Je n'est pas utilisé la phrase "Alice tire ses deux nombres uniformément dans l’intervalle[0,1]", car , en prenant cette phrase à la lettre, lorsqu'une variable aléatoire suit une loi uniforme continue, la probabilité de choisir une valeur isolée est nulle...ce qui ne peut pas convenir ici...!
-
Ddut dernière édition par
Bonsoir Mtschoon, désolé pour ma réponse tardive.
Je trouve pour le gain 0,60,5 + 0,40,5= 0,5 est-ce bien la valeur du gain que je suis censé trouver?La question "Évaluez le gain de cette stratégie lorsque Alice tire ses deux nombres uniformément dans l’intervalle[0,1]." était indépendante de la première. Je n'ai pas compris pourquoi elle n'était pas possible
Merci
-
mtschoon dernière édition par mtschoon

Dut, bonjour,
Ta réponse "le gain 0,6.0,5 + 0,4.0,5= 0,5" n'est pas ce qui est attendu,car tu dois chercher la stratégie pour que Bob donne une réponse exacte avec une probabilité strictement supérieure à 0.5
Utilise l'arbre que je t'ai donné
a et b doivent satisfaire l'inégalité : 0.6a+0.4b>0.5\boxed{0.6a+0.4b\gt 0.5}0.6a+0.4b>0.5 ou, si tu préfères 6a+4b>5\boxed{6a+4b\gt 5}6a+4b>5un exemple qui convient : a=0.3 et b=0.9
(0.6×0.3)+(0.4×0.9)=0.54(0.6\times 0.3)+(0.4\times 0.9)=0.54(0.6×0.3)+(0.4×0.9)=0.54.
On a bien 0.54 > 0.5
un autre exemple qui convient : a=0.5 et b=0.7
(0.6×0.5)+(0.4×0.7)=0.58(0.6\times 0.5)+(0.4\times 0.7)=0.58(0.6×0.5)+(0.4×0.7)=0.58 .
On a bien 0.58 > 0.5Pour ta dernière question, je ne t'ai pas dit que ce n'était pas possible, je t'ai dit que ma proposition ne répond pas exactement à la formulation de cette question.
J'ignore si tu as un cours sur les variables aléatoires ayant une loi continue uniforme sur [0,1]
Si c'est le cas, tu dois savoir que la probabilité de choisir une valeur isolée est nulle. On ne peut procéder que par encadrements .
Par exemple, un nombre étant choisi entre 0 et 1, la probabilité qu'il soit compris entre 0,3 et 0,5 est égale à 0,5 – 0,3, soit 0,2.Si tu n'as pas de cours sur les variables ayant une loi continue uniforme , l'énoncé n'envisage peut-être que des lois discrètes ...ce qui est l'idée de ma proposition.
C'est tout ce que je te dirai sur cette dernière question...