Basse-Cour

Bonjour, j'ai un exercice pour Lundi dont je ne comprend pas ...

Un agriculteur souhaite réaliser un enclos rectangulaire contre un mur pour ses poules. Il dispose de 21 m de grillage et doit tout utiliser.

**** Image à replacer correctement sur le serveur du forum ******L'objectif de cet exercice est de déterminer les dimensions de l'enclos afin que son aire soit maximale.

On note l et L respectivement la largeur et la longueur de l'enclos, en mètres.**a.**Quelles sont les valeurs possibles de l ?**b.**Écris une égalité avec l et L et déduis-en une expression de L en fonction de l.**c.**Exprime l'aire de l'enclos en fonction de l et L puis en fonction de l seulement.

On note A la fonction qui, à l, associe l'aire de l'enclos correspondant.

Avec l'aide de ta calculatrice ou d'un tableur, complète le tableau de valeurs de la fonction A.Image à replacercorrectementsur le serveur du forum**

d. À l'aide du tableau, décris l'évolution de A(x) en fonction de x et donne un encadrement du
nombre x pour lequel A(x) semble maximal.

e. Complète astucieusement un nouveau tableau de valeurs pour donner une valeur approchée au dixième près du nombre x pour lequel A(x) semble maximal.

f. Déduis-en des valeurs approchées des dimensions de l'enclos d'aire maximale.

Merci d'avance pour votre aide

salut

c'est gentil de poser un énoncé complet comme ça... mais normalement tu es censé poser des questions précises plutôt que nous asséner "j'ai un exercice pour Lundi dont je ne comprend pas"

comme tu t'y prends à l'avance, tu pourras essayer de chercher un peu les questions suivantes :
Citation

a. Quelles sont les valeurs possibles de l ?

b. Écris une égalité avec l et L et déduis-en une expression de L en fonction de l.

c. Exprime l'aire de l'enclos en fonction de l et L puis en fonction de l seulement.
pour au moins préciser ce que tu ne comprends pas, ok ?

Pour la a) Les valeurs possible pour l sont : 3
Pour la b) Je pense à 93 et pour la déduction de l'expression, je ne sais pas ...
Pour la c) lL = 9*3 = 21 et pour l seulement, je ne sais pas non plus

Bonjour,

Tes images sont illisibles ! Lire Insérer une image dans son message qu'on trouve en rouge dans la page d'accueil

Les valeurs possibles ne seraient pas très nombreuses ! La valeur 3 seulement ? ! ?

Oui, mais c'est cela que je ne comprend pas très bien ...

Bonjour Sylvain,

Je ne vois pas tes images, "contre un mur" donc je suppose que le mur fait économiser une longueur de grillage.

Tu disposes de 21m de grillage.

Avec ces 21m, il va falloir cloturer 1 longueur et 2 largeurs il me semble.
En plus, il faut utiliser la totalité de ces 21m, ça doit te permettre d'écrire quelques conditions mathématiques non ?

PS : utilises le lien du post de Zorro 18:33 pour insérer tes images correctement.

Pour la 1ere Image avec l'enclos :

**** Image à replacer correctement sur le serveur du forum ******Pour tes trucs, merci, mais je ne vois pas comment je pourrais faire .
Mais j'ai une idée : 9 de longueurs et 12 de largueur

Même en copiant ton lien dans la barre IE, j'ai un message d'erreur.

Je doute qu'avoir une idée suffise et le "mes trucs" ça passe assez mal. Je considère cette façon de s'exprimer limite comme un manque de respect. Tu t'adresses à des adultes, soigne ton expression, ok ?

Les 21m doivent constituer 1 longueur et 2 largeurs de grillage.

Quelle égalité peux-tu écrire ?

Utilise la nouvelle option du forum pour insérer ton document. "Ajoute une image" sous la fenêtre de saisie.

Désolé, je ne pensais pas que vous le prendriez mal ...

**** Image à replacer correctement sur le serveur du forum ******Pour ce qui est de l'égalité, je ne vois pas désolé ...

Le grillage est composé d'une longueur L et de 2 largeur l.

La longueur totale du grillage est donc de L+l+l sois L+2l

Or on utilise la totalité du grillage dont on dispose, soit 21M.

D'où l'égalité :

L + 2l = 21

Ah d'accord ... en fait c'était pas si compliqué que ça

Donc L+2l va me servir pour mon calcul du a), b) et c) ?

Le prendre mal , c'est normal ! On se décarcasse pour écrire des consignes et de conseils pour que ce forum reste convivial et agréable pour tout le monde, ceux qui posent des questions et ceux qui aident.

Alors quand on voit que ce qu'on a écrit n'est pas lu , on n'apprécie pas vraiment ! Si tu écrivais toute une page dans un devoir et que ton prof ne la lise pas , sans raison , tu n'apprécierais pas !

Bonjour

a. Quelles sont les valeurs possibles de l ?

La clôture est constituée de deux largeurs et d’une longueur de grillage.

l peut prendre comme valeur 1m , 2m etc . . . mais par ex l=15m, ce ne sera pas possible (longueur grillage insuffisante). Il y a un intervalle de valeurs possibles pour l qu’il te faut déterminer.

Réfléchis au passage à ce que va représenter cet intervalle pour la fonction A des questions suivantes.

b. Écris une égalité avec l et L et déduis-en une expression de L en fonction de l.

On a vu que :

L+2l = 21

A toi d’exprimer l en fonction de L à partir de cette égalité.

La suite, tu devrais t’en sortir je pense. Tu définis proprement la fonction avec tous les ingrédients nécessaires et les bonnes notations.

je prend 7m pour la largueur l, il me restera 14m pour la longueur L, donc 7l+14L = 21 ?

Sylvain88
je prend 7m pour la largueur l, il me restera 14m pour la longueur L, donc 7l+14L = 21 ?

Tu peux prendre l=7m et L=14m alors tu as utilisé 14+2×7 soit 28m de grillage.

Or tu ne disposes que de 21m de grillage.

Si prends l=7m, alors il reste 21-2×7=7 m pour la longueur non ?

Bonjour,

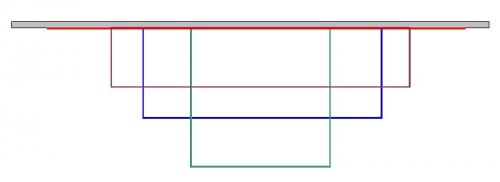
$fichier math$

Pour la question 1) ce petit schéma peut t’aider à encadrer les valeurs possibles pour la largeur l.

Ces 4 clôtures utilisent 21m de grillage. La rouge correspond à l=0m, la violette à l=3m, la bleue à l=4,5m et la verte correspond à la valeur maxi de l ... si on veut que la largeur l reste inférieure à la longueur L.

Edit : Modification du schéma pour que l ≤ L.