Triangle rectangle et Pythagore

Bonjour à tous, j'ai un soucis avec un exercice concernant 2 triangles

d'après les données on doit prouver que le triangle ABC est rectangle en A.
on sait que (DE) et (AC) sont parallèles et que les points C, B et E sont alignées et le triangle BDE est rectangle en D.

$fichier math$
je suis en 4eme et nous n'avons fait que le chapitre sur Pythagore. on a pas encore fait Thalès ni les triangles dans les cercles alors je n'arrive pas à prouver que le triangle est rectangle en A.

on a bien BD²+ DE²=BE² mais je n'ai aucune mesure alors comment prouver

je vous en remercie .

Bonjour,
Il manque une donnée : les points A,B,D sont-ils alignés ?

on ne le sait pas mais quand on regarde la figure les points ne sont pas alignées , donc je ne peux pas utiliser Thalès .

Relis ton énoncé.
Si les points A,B,D ne sont pas alignés, alors ABD ne peut pas être rectangle en A ( ni en C ).

mon exercice commence comme cela :démontrer, que le triangle ABC est un triangle rectangle en utilisant les informations fournies et j'ai la figure que j'ai mis enimage .....

Vérifie quand même que tu n'as rien oublié, que ta figure est entière.
Comme je te l'ai dit, si A,B,D ne sont pas alignés, le triangle ABC n'est pas rectangle.

je n'ai absolument aucune autre donnée sa part cette figure et l'énoncé que je vous ai ecris

je ne sais pas si vraiment A, B et D sont alignés j'en ai déduis sur la feuille où il ne sont pas alignés.

peut etre qu'ils sont alignés mais rien ne nous le dis ....

et même si les points A,B,D sont alignés comment faire je n'ai pas encore appris le théorème de Thalès .... et ce n'est aps l'objet de mon devoir qui est basé sur le théorème de Pythagore.

Prolonge la droite (BD) jusqu'à son intersection avec la droite (AC) : en A'.
C'est A'BC qui est rectangle : vois-tu pourquoi ?

mais dans l'énoncé on parle bien du triangle ABC qui doit être rectangle en A on ne parle pas de A'

je vous remercie des réponses apportées mais ca ne résout pas que je dois prouver que le triangle ABC est rectangle en A.

salut

tout ce que tu peux dire, c'est que les angles $bed^\small\widehat{bed}$ et $bca^\small\widehat{bca}$ sont égaux comme alternes-internes vis-à-vis des parallèles (DE) et (AC).

malheureusement, il est vrai qu'en caricaturant un peu, on pourrait très bien avoir la situation suivante :

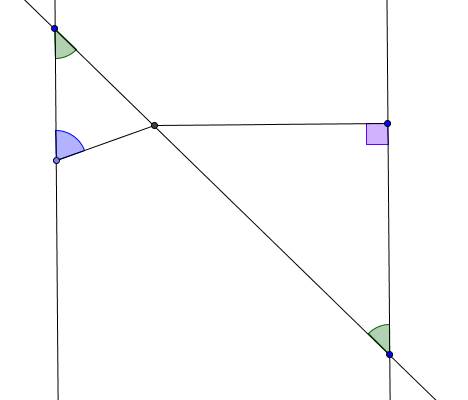
les deux angles verts sont égaux, mais il est possible que le bleu ne soit pas droit !

Je te l'ai dit: si A,B,D ne sont pas alignés, ABC n'est pas rectangle.
Je ne peux rien faire de plus.

j'ai revu ma prof de math aujourd'hui qui m'a dit de ne pas utiliser Thales et ques les points A, B et D ne sont pas ALIGNES !!

est ce que si je dis comme d'après la figure on a le triangle DBE rectangle en D on a (DE) et (BD) perpendiculaires et que comme les points C, B et E sont alignées et que (DE) et (AC) sont parallèles on peut donc dire que (CA) et (AB) sont perpendiculaires et donc le triangle ABC est rectangle en A ?