Deux exercices sur la configuration de thalès
-
Bboomboompow dernière édition par
Bonjour a tous
voila 2 exercices a faire où je ne comprends RIEN

les exercices sont les n°67 p 236 et 71p 237 du livre Transmath 3ème tome 2
exercice n°67
Le cercle de centre A a pour rayon 2cm et e cercle B a pour rayon 3 cm et P aux deux cercles coupe en O le segment [AB]
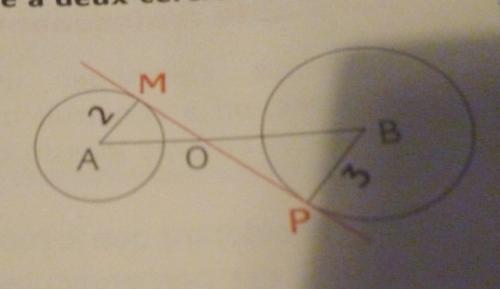
a) Démontrer que les triangles OAM et OBP forment une configuration de Thalès
b) Calculer OA et OB
exercice n°71
Les points O,A et A' sont alignés. Les points O, B et B' sont sont alignés. Les Points O, C et C' sont alignés.
les droites (AB) et (AB'), ainsi que les droites (CB) et (C'B') sont parallèles
Démonter que les droites (AC) et (A'C') sont parallèles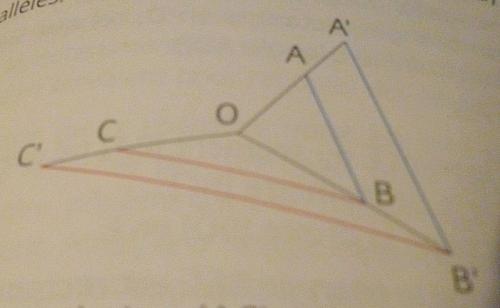
merci d'avance

[Affichage des figures rendu conforme aux normes du site. NdZ]
-
Zauctore dernière édition par

salut
[résolu : le pb d'affichage de tes figures scannées]
pour le 1er : explique déjà pourquoi (AM) et (BP) sont parallèles ; ensuite applique le théorème direct à la "configuration papillon" (attention au sommet, c'est O).
pour le 2e, je dis juste : réciproque du théorème de Thalès : il suffit que tu prouves que OA/OA' est égal à OC/OC'