Les fonctions associées

Bonjour à tous encore une fois , j'ai un autre soucis concernant cet exercice : Si vous pourriez m'aider , ca serait gentil ..

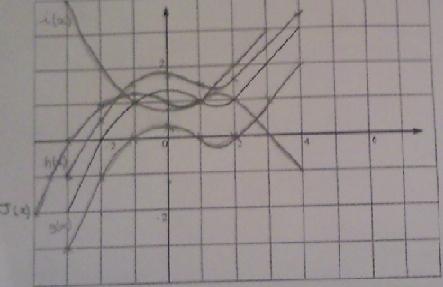
On a représenté si dessous une fonction f sur [-3;4] on définit les fonctions :
g(x)=f(x)-1
h(x)=0.5f(x)
i(x)=f(x)+2
j(x)=f(x-1)

Donc j'ai représenté les fonctions définies sur le repère suivant (je ne sais pas si elles sont correctes.. :/)

Et après il faut expliquer comment on passe de Cf à Cg , Ch , Ci et Cj ..
C'est sur cette question qu'il me faudrait de l'aide s'il vous plait..

Merci d'avance , Bisous .

oups si je ne donne pas le graphique ça risque d'être compliqué ^^

$fichier math$

donc la fonction f toute seule c'est celle qui passe par A (-2;0)

La courbe représentant f , $C_f$ , est donc celle qui est ""l'avant dernière"" , en partant du bas

avec g(x) = f(x) - 1 , on obtient les ordonnées de g(x) en enlevant 1 à celles des points de $C_f$

Or f(-2) = 0 donc g(-2) = f(-2) - 1 = 0 - 1 = 1 ; donc $C_g$ passe par le point de coordonnées (-2 ; 1)

Pour i(x) = f(x) + 2 , on obtient les ordonnées de g(x) en ajoutant 2 à celles des points de $C_f$

Or f(-2) = 0 donc i(-2) = f(-2) + 2 = 0 + 2 = 2 ; donc $C_i$ passe par le point de coordonnées (-2 ; 2)

Tu essayes les autres sur le même principe

Je ne comprend pas à quoi ça sert ce que tu fais là ?

Cela sert à trouver quelles sont les représentations de g , h , i et j !!!!!

Quelle translation te permet de passer de $C_f$ à $C_g$ ?

Quelle translation te permet de passer de $C_f$ à $C_i$ ?

ah ok , et donc ça fait quoi à chaque cas ..

.... je ne comprends pas ta question !

Tu passes de $C_f$ à $C_g$ en déplaçant $C_f$ de quelle manière ?

Je viens juste de finir un DM sur ça, en clair pour les justifications on pourait avoir quelque chose comme ça:

La courbe Cg de la fonction g définie par g(x) = f(x+a) est la translatée de la courbe Cf par la translation de vecteur -ai soit a unités vers la gauche. (Si g(x) = f(x-a) alors c'est une translation de vecteur ai soit a unités vers la droite)

La courbe Cg de la fonction g définie par g(x) = f(x) + a est la translatée de la courbe Cf par translation de vecteur aj soit a unités vers le haut. (Si g(x) = f(x)-a alors c'est une translation de vecteur -aj soit a unités vers le bas)

La fonction g définie par g(x)= a.f(x) à le même ensemble de définition que la fonction f. Pour obtenir sa courbe Cg, il faut qu'à chaque abscisse on multiplie par a l'ordonnée du point de Cf.

Je pense ne pas me tromper sur les justifications, maintenant, il faut juste remplacé a par le chiffre qu'on souhaite. (Après tout, c'est dans mon livre de Maths ^^)