Résolution d'égalités avec fonctions trigonométriques et mesures d'angles

bonjour

j'ai cet exercice a faire que j'ai commencé mais apres je bloques

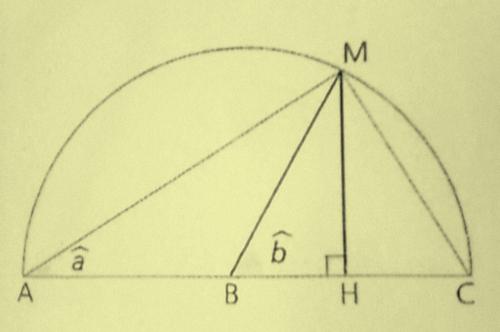
le demi-cercle ci-dessus de centre B et de diametre [AC] a pour rayon 1

demontrer les egalites suivantes : cosâ = AH/AM cosâ = AM/AC AH = 1 + cosb

en deduire l'égalité : cos²â = 1 + cosb/2

j'ai fait ca : dans le triangle AMC le point M est situé sur le cercle de diametre [AC].si M est un point quelconque du cercle du diametre [AC] alors le triangle AMC est rectangle en M
dans le triangle AMC rectangle en M : cosâ = AM/AC

dans le triangle AMH il y a un angle droit donc c'est un triangle rectangle
dans le triangle AMH rectangle en H : cosâ = AH/AM

A B H sont alignés dans le meme ordre donc AH = AB + BH = 1 + BH
comme le diametre de [AC] est de rayon 1 alors AB = 1

dans le triangle BMH rectangle en H :cosb = BH/BM

AH = 1 + cosb
AH = AM * cosâ
AM * cosâ = 1 + cosb

2 * cosâ * cosâ = 1 + cosb
2 * cosâ = 1 + cosb
cos²â = 1 + cosb /2

2)comparer les mesures des angles â et b

en deduire que pour tout angle â dont la mesure est comprise entre 0° et 45° l'égalté cos²â = 1 + cos 2â/2 est vérifiée

la je bloque $fichier math$

Bonjour,
Quelle est la nature de l'angle a , et celle de l'angle b ?

mathtous
Bonjour,
Quelle est la nature de l'angle a , et celle de l'angle b ?

mesure de l'angle aigu et b un angle optu

Non : b est aigu aussi.
Mais ce n'est pas ce qui importe : que peut-on dire de chacun de ces angles vis à vis du cercle ?

Où est situé le sommet de l'angle b ?
Alors quel nom donne-t-on à cet angle ?

mathtous
Où est situé le sommet de l'angle b ?
Alors quel nom donne-t-on à cet angle ?

â est un angle inscrit dans le demi-cercle et qui intercepte l'arc MC

b est un angle au centre du demi-cercle qui intercepte le meme arc alors l'angle au centre mesure le double de l'angle inscrit

ABM est un triangle isocele de sommet M donc : BMA = BAM d'ou BMA = â
MBC est un triangle isocele de sommet B donc : BMC = BCM

la somme des angles d'un triangle vaut 180° donc : BMC + BCM + B = 180°

donc BMC + BCM = 180° - b

BMC = BCM donc BMC + BCM = 2BMC

2BMC = 180° - b

BMC = 90° - b/2

l'angle AMC est droit donc : AMB + BMC = 90°

AMB = 90° - BMC

AMB = 90° - (90° - b/2) = b/2

d'ou b = 2a

donc cos²â = (1 + cosb)/2

C'est trop compliqué.
Citation
â est un angle inscrit dans le demi-cercle et qui intercepte l'arc MC

b est un angle au centre du demi-cercle qui intercepte le meme arc alors l'angle au centre mesure le double de l'angle inscrit
Citation
d'ou b = 2a

donc cos²â = (1 + cosb)/2
Cela est suffisant

mathtous
C'est trop compliqué.
Citation
â est un angle inscrit dans le demi-cercle et qui intercepte l'arc MC

b est un angle au centre du demi-cercle qui intercepte le meme arc alors l'angle au centre mesure le double de l'angle inscrit
Citation
d'ou b = 2a

donc cos²â = (1 + cosb)/2
Cela est suffisant

d'accord merci

De rien.
A+

louann
mathtous
C'est trop compliqué.
Citation
â est un angle inscrit dans le demi-cercle et qui intercepte l'arc MC

b est un angle au centre du demi-cercle qui intercepte le meme arc alors l'angle au centre mesure le double de l'angle inscrit
Citation
d'ou b = 2a

donc cos²â = (1 + cosb)/2
Cela est suffisant

d'accord merci

application

a) sachant que cos30° = V3/2 demontrer que cos²15° = 2 + V3 /4

B) verifier que cos 15° = V6 + V2 /4 ( le V c'est racine carrée)

a) cos²15° = 1 + V3/2

2
= 2 + V3/2

2

= 2 + V3

2

1

= 2 + V3

2
*1/2 = 2 + V3 /4

B) cos15° = (V6 + V2)² /4 = 6 + 2 /4 = 8/4 = 2