Nombre d'or et Khéops

Bonjour tout le monde, j'ai un Dm à finaliser pour demain matin.

C'est sur la pyramide de Khéops et le nombre d'or . Beaucoup de topics ont été crées sur ce sujet, mais aucun ne répondait à mes questions .
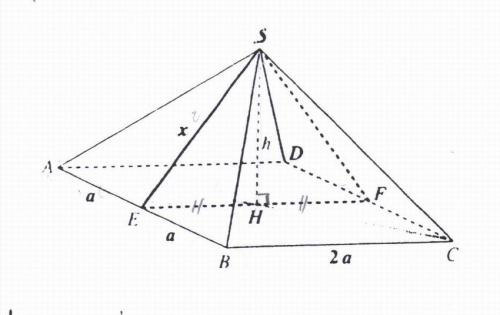
D'après Hérodote, Khéops, de base carrée sont les surfaces latérales sont des triangles isocèles possède la propriété suivante :
" Les surfaces latérales triangulaires ont une aire égale à celle du carré construit sur la hauteur de la pyramide " .

Exprimer h en fonction de a et de x. J'ai trouvé ( h²=x²-a²)
Exprimer en fonction de a et de x l'aire du triangle SAB et celle du carré de côté SH . J'ai trouvé . ( aire SAB= xa ; et aire carré coté SH= h²)
En utilisant la remarque d'Hérodote, en déduire la relation liant a et x . Je n'y arrive pas
Montrer que cela implique alors que ES/EH= φ . Je n'y arrive pas non plus

Merci d'avance $fichier math$

1°) $h$ ^2 $= x$ ^2 $a^2$
2°) Aire(SAB)=xa et Aire(carré côté $S H) = x$ ^2 $a^2$ (Cf la question : en fonction de a et x)
3°) Traduire la propriété "Les surfaces latérales triangulaires ont une aire égale à celle du carré construit sur la hauteur de la pyramide"
avec les données du texte.
4°) ES/EH=x/a
...

3°) Je ne comprends pas comment traduire avec les données du texte !
J'avais pensé à marquer ax=x²-a²
ce qui donne x²-a²-ax=0. Est ce cela ,?

Et pour la dernière j'avais en effet compris que ES/EH = x/a, mais je ne vois pas à quoi cela me mène . Pouvez vous développer davantage ??

3°) Je ne comprends pas comment traduire avec les données du texte !
J'avais pensé à marquer ax=x²-a²
ce qui donne x²-a²-ax=0. Est ce cela ,?

Et pour la dernière j'avais en effet compris que ES/EH = x/a, mais je ne vois pas à quoi cela me mène . Pouvez vous développer davantage ??

3°) oui voilà mais écrire plutôt x²-ax-a²=0 (on ordonne suivant les puissances décroissantes de x)
4°) en divisant l'égalité x²-a²-ax=0 par a²≠0, on obtient ...

D'accord donc la 3) la relation c'est juste x²-ax-a²=0, je met ça et ça convient .

On obtient pour la 4) en divisant par a²:
ɸ²-1-ɸ=0
et après ?

?

je répète !
4°) en divisant l'égalité x²-a²-ax=0 par a²≠0, on obtient ...

D'accord donc la 3) la relation c'est juste x²-ax-a²=0, je met ça et ça convient .

On obtient pour la 4) en divisant par a²:
ɸ²-1-ɸ=0
et après ?

ou bien (x/a)²-1-(x/a)=0

ou bien (x/a)²-1-(x/a)=0

tu es têtue toi !
je re-répète !
4°) en divisant l'égalité x²-a²-ax=0 par a²≠0, on obtient ...

Pythagoricienne
(x/a)²-1-(x/a)=0
voilà !
donc x/a est une solution (positive) de l'équation X²-X-1=0
équivalente à X²=X+1
...

Oui, mais ej ne vois toujours pas en quoi ça prouve que ES/EH doit être égal au nombre d'or .

Pythagoricienne
Oui, mais ej ne vois toujours pas en quoi ça prouve que ES/EH doit être égal au nombre d'or .
que connais-tu du nombre d'or ?

Je sais que le nombre d'or est égal à( 1+√5)/2.
J'ai eu plein d'exercices avant celui-ci avec ses propriétés algébriques, la section d'or, la suite de fibonacci ...

Mais en fait je comprends ce que vous me dîtes, mais cela répond-il à la question " Montrer que cela implique alors que ES/EH=φ" ??

Pythagoricienne
Je sais que le nombre d'or est égal à( 1+√5)/2.
J'ai eu plein d'exercices avant celui-ci avec ses propriétés algébriques, la section d'or, la suite de fibonacci ...
Mais en fait je comprends ce que vous me dîtes, mais cela répond-il à la question " Montrer que cela implique alors que ES/EH=Φ" ??
En fait en 3ème tu vas dire oui parce que tu "sais" que Φ est le seul nombre positif tel que Φ²=Φ+1 (mais je ne pense que ce résultat a été démontré vraiment)
donc x/a=Φ

sinon en débordant un peu le programme on peut essayer de résoudre l'équation X²-X-1=0

Ok, donc en conclusion que me conseillez vous de mettre comme réponse à la question 4 ?

bah ce que l'on vient de dire !

C'est à dire ?
Je en le fais pas exprès, je ne vois pas le lien .

4°) en divisant l'égalité x²-a²-ax=0 par a²≠0, on obtient ...
donc x/a est une solution (positive) de l'équation X²-X-1=0
équivalente à X²=X+1
or Φ est le seul nombre positif tel que Φ²=Φ+1
donc ...

maintenant je ne sais pas si
"Φ est le seul nombre positif tel que Φ²=Φ+1"
est un résultat que tu connais ? que tu as démontré ?