aide pour dm géométrie et droites perpendiculaires
-
Ssophiie dernière édition par
bonjour,
ABCD est un rectangle tel que AB=4cm et BC=3cm.
M est un point de [AB] tel que AM= 1cm
N est un point de [BC] tel que BN= 1 cm
a) Démontrer que les droites (MD) et (MN) sont perpendiculaires.
b) La droite perpendiculaire à (DN) et passant par M coupe [DN] en H. Calculer MH.j'ai trouver pour le a) mais je n'y arrive pas pour le b)
-
Zorro dernière édition par

Bonjour,
Pourrais-tu enfin
-
mettre tes sujets dans le même forum !
-
choisir un titre qui respecte les consignes !
Tu m'éviteras du travail inutile et j'en aurai plus pour t'aider :razz:
-
-
BBertoche dernière édition par
b) il y a des triangles rectangles un peu partout sur cette figure donc Pythagore Pythagore Pythagore ... et peut-être aussi Pythagore !
-
Zorro dernière édition par

Il et de quel niveau celui-là : 4ème ou seconde ? ? ?
-
Ssophiie dernière édition par
c'est un exercice de 4ème
-
Ssophiie dernière édition par
pourriez-vous m'aidez ??? s'il vous plait c'est urgent c'est pour demain
je m'escuse de ne pas avoir mis le bon titre et de n pas l'avoir mis au bon endroit je le retiens pour la prochaine fois
-
IIron dernière édition par
bonjour Sophiie,
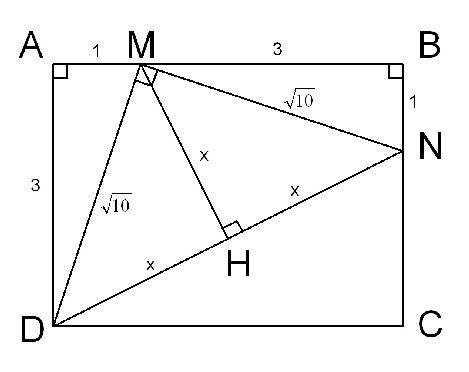
Avec Pythagore, tu as dû obtenir DM = MN = √10 cm
dans la question a) tu as montré que l'angle DMN = 90°
Le triangle DMN est donc rectangle et isocèle en M
La droite (MH) est une hauteur du triangle issue du sommet M (et aussi bissectrice de DMN et médiatrice de [DN] d'ailleurs)
Dans ce cas particulier, tu as DH = MH = NH
Si tu appelles x ces longueurs (MH = x).
Pour la trouver, tu peux appliquer Pythagore dans le triangle MNH (par ex) rectangle en H
MN² = MH² + NH² soit
(√10)² = x² + x²
(√10)² = 2x²
Est-ce que tu sais résoudre ça en 4ème. Ca me parait compliqué ... mais cet exo me semble bien difficile pour ton niveau. A moins que je ne sois passé à coté d'une solution simple.
-
Ssophiie dernière édition par
bonjour, merci de votre aide mais je ne comprend pas du tout. L'exercice vient d'un livre de 4ème.
-
Oovergamebac dernière édition par
a) Si deux droites dont parallèle à une même troisième alors elle est perpendiculaire.
Donc ABCD rectangle = angle droit
BC = AD et AB = DC
Donc BN perpendiculaire à HN et à AB.b) ABCD est un rectangle donc les côtés opposés d'un rectangle sont de même mesure.
Donc AB=DC et BC=AD
Donc BN = AH et AD= le point qui coupe le segment DCNous avons une nouvelle figure : AMH (triangle rectangle)
Le triangle AMH est un triangle rectangle en A (angle droit du rectangle) donc on peux utiliser le théorème de Pythagore.
HMHMHM^2=AH2=AH^2=AH2 + AM2AM^2AM2
HM2HM^2HM2= 1 + 1
HM2HM^2HM2= 2
HM = √2 cm (valeur exacte)
HM vaut √2 cm (hypoténuse)
-
IIron dernière édition par
Bonjour overgamebac,
Citation
Donc BN perpendiculaire à HN et à ABSi (BN) est perpendiculaire à (HN) et à (AB) alors (HN) serait parallèle à (AB), ce qui n'est pas le cas.
Citation
AMH (triangle rectangle)
De mon coté, j'ai cette figure :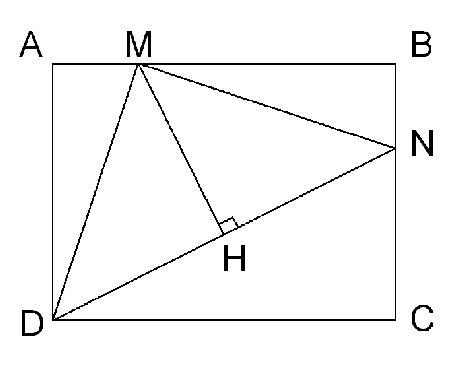
-
IIron dernière édition par
Bonjour sophiie,
Mon charabia d'hier est-il plus clair avec cette figure ?