Cout total et bénéfice

bonjour a vous tous, voici un de mes exercice de math à faire, j'y réfléchi depuis pas mal de termps jai quelques idées, mais je ne suis vraiment pas sur, et pour certaine question je n'en ai aucune idées!! aidé moi svp! merci pur votre aide! voici l'exercice en question:

Le coût total de fabrication de x milliers d’articles est C(x) = x²+ 2x + 28,75 (le coût est exprimé enmilliers d’euros) avec x appartient ]0; 12].On admet que chaque article fabriqué est vendu au prix unitaire de 16euros. La recette exprimée enmilliers d’euros pour la vente de x milliers d’articles est donc R(x) = 16x.La figure ci-dessous, donne la courbe représentative de la fonction coût total dans un repère orthogonal.

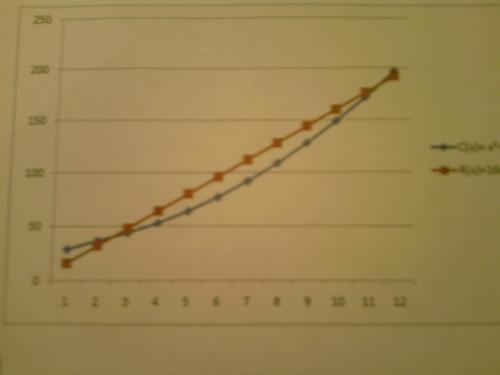
$fichier math$

Par lecture graphique, déterminer la plage de production qui permet de réaliser un bénéfice.
On note B(x) le bénéfice réalisé, lorsque l’entreprise produit et vend x milliers d’articles.
a. Montrer que le bénéfice exprimé en milliers d’euros, lorsque l’entreprise produit et vend x
milliers d’articles, est donné par B(x) = −x2 + 14x − 28,75 avec x 2 ]0; 12].
b. Étudier les variations de la fonction B sur ]0; 12]. En déduire la quantité d’articles à produire et
à vendre pour que le bénéfice soit maximal. Quel est le montant en euros du bénéfice maximal ?
c. Étudier le signe de B(x). En déduire la plage de production qui permet de réaliser un bénéfice
(positif).

la courbe bleu représente c(x)=x²+2x+28.75
la courbe rouge représente r(x)=16x

Bonjour,

un bénéfice est réalisé si la recette est supérieure au coût de fabrication, cad quand la courbe de couleur ... est au dessus de la ...

2a) Bénéfice pour x milliers d’articles vendus = Recette pour x milliers d’articles vendus - Coût de fabrication de x milliers articles

donc B(x) = ... - ...

2b) B(x) = −x2 + 14x − 28,75 avec x ∈ ]0; 12]

Pour étudier les variations de B(x), tu peux passer par la dérivée (je ne pense pas que tu l'ais vue en cours).

Sinon, c'est un polynôme du second degré dont le coefficient de x² est négatif, sa représentation est donc une ... tournée vers le ... dont tu es capable de déterminer le sommet.

2c) Tu trouves les racines (si elles existent) et tu détermines le signe de B(x) à l'intérieur puis à l'extérieur des racines.

Bon courage

je te remercie, j'avais réfléchi a quelques questions, et je retrouve quelques une de mes réponse, ce qui prouve que je ne suis pas si nul que ca !! ca rassure! en tout cas merci pour ton coup de pouce! et peut etre a une prochaine!!

excuse moi, pour la b pour calculer le sommet, on fait bien -b/2a? du cout on trouve x=7, et on peut trouver la quantité d'article(=y) en fonction de x. f(7)= 118.25 . sauf que j'ai un souci, c'est que sur ma réprésentation je trouve bien x=7, mais y pas du tout.

et pour la c) peux tu m'expliquer? je comprends pas !

bon pour la b) finalement j'ai reussi à comprendre, par contre pour la c) toujours pas

Bonjour,

b) Le sommet est bien atteint pour x=7 ... l'unité est en milliers d'articles.

Le bénéfice maxi est atteint pour 7000 articles fabriqués.

Le bénéfice maxi correspond à B(7) = 20.25 milliers d'euros soit 20 250 €

sauf erreur de ma part

c) Tu calcules le discriminant, s'il est positif, le polinôme B(x) admet 2 racines distinctes que tu calcules également.

un polynôme du 2nd degré de la forme ax² + bx + c est du signe de a à l'extérieur des racines et du signe de -a à l'intérieur des racines.

Ici a = ...

Tu détermines l'intervalle des x pour que B(x) soit positif.