produit de séries à termes positifs

Bonjour , j'ai vraiment besoin d'aide

Voici l'énoncé

Soient(n≥0) ∑ $a_n$ et(n≥0) ∑ $b_n$ deux séries convergents à termes positifs

Soit $C_n$ = $a$ _0 $b_n$ +...+ $a$ k $b</em>{n-k}$ +... $+ a$ _n $b_0$ .

On dit que (n≥0) ∑ $C_n$ est la série produit de (n≥0) ∑ $a_n$ et (n≥0) ∑ $b_n$

Montrer que pour tout entier n

$∑k=0nck≤(∑k=0nak)(∑k=0nbk)≤∑k=02nck\sum_{k=0}^n c_k \leq \left(\sum_{k=0}^n a_k\right)\left(\sum_{k=0}^n b_k\right) \leq \sum_{k=0}^{2n}c _k$
Montrer que ∑ $C_n$ est convergente et calculer sa somme !

EUhh je ne sais pas comment faire :frowning2:

merci de votre aide

Bonsoir

je peux te montrer un argument "géométrique", en disposant les termes dans un tableau illimité en quelque sorte

comme j'ai un peu la flemme de faire du latex, je te montre un scan d'un de mes docs - à un changement de notations près ça illustre bien l'idée de la preuve de la double inégalité :

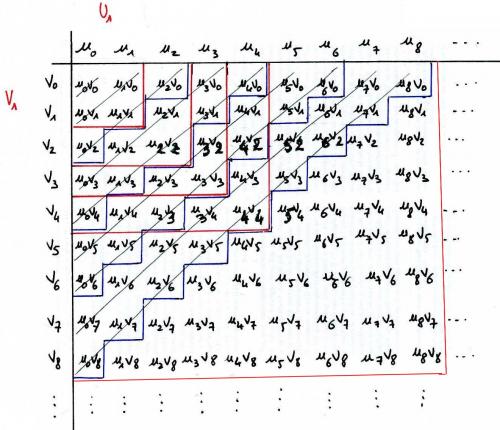
$fichier math$

le carré de u_0v_0 à u_4v_4 contient tous les produits u_i v_j avec i, j inférieurs à 4 donc à plus forte raison tous les produits u_i v_j avec i, j inférieurs à 4 avec la restriction i+j = 0, 1, 2, 3 ou 4 (sommation diagonale)

mais ce carré est contenu dans le triangle limité par la diagonale de u_8 à v_8 dont la somme des termes est

$∑k=02×4ck\sum_{k=0}^{2\times4} c_k$
Bien entendu on peut rédiger ça avec n... on peut même se dispenser de faire le moindre schéma (cf cours de mathématiques supérieures, tome 1, IV-3-2 par v. smirnov, éditions mir).

Mais c'est quand même plus clair, surtout pour retenir le résultat d'encadrement :

$fichier math$

Pardon, le schéma qui illustre l'encadrement demandé est plutôt celui-ci :
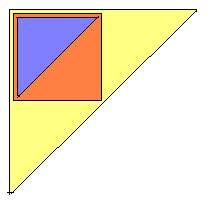
$fichier math$
j'ai posté trop vite hier soir !
En orange, on trouve le produit (a_0 + a_1 + ... + a_n)(b_0 + b_1 + ... + b_n).

merci beaucoup de vos efforts ...
mais je suis pas sur d'avoir tout compris: chauqe diagonale ( ce qui est barré) correspond au produit , c'est cela?
Ensuite pour l'encadrement je ne vois pas comment le rédiger ( le livre que vous me proposez est introuvable!)

ce qui est barré c'est exactement la suite des termes de la série-produit. on vous a pas expliqué ça en classe, la sommation "à la Cauchy" ? je crois que c'est de lui.

pour la preuve, c'est essentiellement un pb de développement : $(a0+...+an)(b0+...bn)\small (a_0 + ... + a_n)(b_0 + ... b_n)$ contient dans son développement tous les termes $aibj\small a_ib_j$ avec i, j inférieurs à n. donc à plus forte raison tous les termes de la somme partielle $∑k=0nck\small \sum_{k=0}^n c_k$ .

ça donne la 1re inégalité.

tiens, j'ai retrouvé le livre en question (j'en suis l'heureux possesseur d'un exemplaire !), je m'efface derrière Vladimir (tu verras il débute par mentionner des séries absolument convergentes pour ensuite traiter essentiellement des séries à termes positifs).

$fichier math$
Bonne lecture

Merci bien
On ne l'a pas vu en classe!! il nous le donne en TD !!
Encore merci