DM avec relations trigonométriques : sin 2a = 2 sin a cos a en 3e !

[eards]

Bonsoir à tous,
j'ai aujourd'hui terminé mon DM de maths, cependant il me reste 1 exercice qui me bloque fortement. J'ai beau essayé de tous les côtés , je trouve pas.
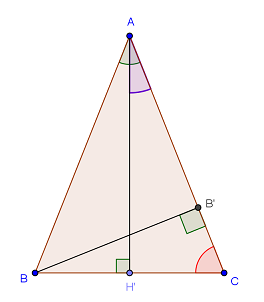
Donc voilà la bête :

On considère un triangle ABC isocèle en A avec AB = AC = 1dm et tel que l'angle BÂC soit aigu.

On note A' le pied de la hauteur issue de A et B' celui de la hauteur issue de B.

1. Faire une figure puis exprimer en fonction de a= A'ÂC la mesure des angles BÂC et B'BC.

2. Démontrer les trois égalités suivantes : BB'= sin 2a ; BB' = BC x cos a et BC = 2sin a (en dm)

3. Déduire , des trois résultats précédents, l'expression de sin 2a en fonction de sin a et cos a

Je vous remerci d'avance.

[Zauctore]

salut

ça c'est dur en 3e ! mais ça démontre une propriété intéressante que tu retrouveras plus tard (en 1re)...

1. déjà (AA') est la ... de l'angle BÂC

2. ensuite dans BB'A tu peux écrire la définition du sinus de l'angle BÂC qui te donnera la première relation.

3. après, dans AA'C trouve la valeur de l'angle en C

4. après quoi, exprime le cosinus de l'angle BCB' de sommet C dans le triangle BB'C - cela te donnera la 2e relation.

5. pour BC c'est du même genre, mais avec le sinus.

voilà déjà de quoi te mettre sur la voie.

[eards]

1 AA' est la médiane de l'angle BÂC vu quelle le coupe en 2 angles égaux

2. sinus BÂC = B'B/ AB

3. je ne sais pas comment faire

4. cos BCB' = B'C / BC

5. je ne sais pas trop comment faire

[Zauctore]

1. ici médiane = bissectrice : deux angles égaux. (car triangle *isocèle *et sommet principal, etc.)

2. AB = 1 justement

3. somme des angles a + 90 + ... = 180.

4. ah j'suis bête ! faut passer plutôt par l'angle B'BC de sommet B qui est égal à ... ça alors pour le coup ça tombe bien !

[eards]

Bonsoir,
je n'ai absolument rien compris de ce qu'il fallait faire à la fin.
Et je ne vois pas quels réponses que vous me donnez correspondent à mes questions

[Zauctore]

bon alors on reprend...

1. AA' n'est pas que la médiane, c'est aussi la bissectrice, puisqu'elle est issue du sommet principal d'un triangle isocèle

donc BÂC = 2a.

2. sinus BÂC = B'B/ AB = B'B/ 1 = BB' ce qui prouve que sin 2a = BB'.

3. on s'attaque à BB' = BC x cos a.

dans BB'C, l'angle rouge C vaut 90 - a (avec la somme des angles comme j'ai écrit ci-dessus).

maintenant dans BB'C toujours, tu en déduis l'angle B'BC.

il en résultera la relation attendue.

[eards]

-Faire une figure puis exprimer en fonction de a= A'ÂC la mesure des angles BÂC et B'BC. Vous me donnez que l'angle BÂC

-Démontrer les trois égalités suivantes : BB'= sin 2a ; BB' = BC x cos a et BC = 2sin a (en dm). Je ne vois pas comment trouver l'angle B'BC

-Déduire , des trois résultats précédents, l'expression de sin 2a en fonction de sin a et cos a. je ne trouve pas

Je vous remerci d'avance.

[Zauctore]

Bon je vais en donner la solution car le but de l'exercice vaut la peine.

Enoncé
On considère un triangle ABC isocèle en A avec AB = AC = 1dm et tel que l'angle $\widehat{bac}$ soit aigu.

On note A' le pied de la hauteur issue de A et B' celui de la hauteur issue de B.

1. Faire une figure puis exprimer en fonction de $a=\widehat{a^{\prime }ac}$ la mesure des angles $\widehat{bac}$ et $\widehat{b^{\prime }bc}$.

2. Démontrer les trois égalités suivantes (en dm) :

i. $b{b}^{\prime }=\sin 2a$

ii. $b{b}^{\prime }=bc\cos a$

iii. $bc=2\sin a$

3. Déduire , des trois résultats précédents, l'expression de $\sin 2a$ en fonction de $\sin a$ et de $\cos a$

1. La figure :

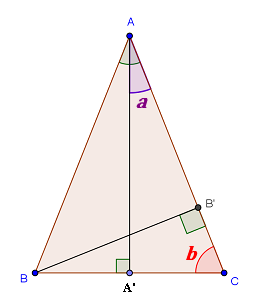
bien entendu $\widehat{bac}=2a$ puisque (AA'), hauteur issue du sommet principal A du triangle isocèle ABC est aussi bissectrice de l'angle.

pour obtenir $\widehat{b^{\prime }bc}$, passons par la détermination de l'angle à la base $b$ dans le triangle ABC. on trouve

$b=(180-2a)/2=90-a$
(il y avait plus simple encore dans le triangle AA'C) ; on en déduit dans BB'C que

$\widehat{b^{\prime }bc}=90-(90-a)=a$

2. i. dans ABB' rectangle, on a

$\sin \widehat{ba{b}^{\prime }}=\frac{b{b}^{\prime }}{ab}\text{donc}\sin (2a)=b{b}^{\prime }$
puisque AB = 1.

ii. dans BB'C on a

$\cos \widehat{b^{\prime }bc}=\frac{b{b}^{\prime }}{bc}\text{donc}bc\times \cos a=b{b}^{\prime }$
(il suffit de multiplier les deux membres de la définition du cosinus par BC pour cela).

iii. on a BC = BA' + A'C = 2 A'C.

or dans le triangle AA'C on a par définition du sinus

$a^{\prime }c=ac\times \sin \widehat{ca{a}^{\prime }}\text{donc}{a}^{\prime }c=\sin a$
d'où finalement

$bc=2\times \sin a$

3. on a deux expressions de BB' :

$b{b}^{\prime }=\sin (2a)\text{et}b{b}^{\prime }=bc\cos a$
d'où

$b{b}^{\prime }=\sin (2a)=bc\cos a$
mais puisque $bc=2\times \sin (a)$ on en déduit

$\small \fbox{\sin(2a) = 2 \times \sin (a) \times \cos a}$
Et voilà !