Besoin d'aide Dm fraction lettre
-
NNekoDown dernière édition par
Salut à tous ,
Alors voila j'ai un gros problème j'ai mon DM de math à rendre Demain et il y a un exo que je ne comprends rien du tout .
Transmath 2007 4ème exo 156 p 57 .
1.une conjecture .
a. Calculer la somme , puis le produis des nombres x et y dans chacun des cas suivants :
x= 7 sur 5 et y=7 sur 2 .
x= 13 sur 9 et y= 13 sur 4 .
x= 9 sur 4 et y= 9 sur 5 .b. Quelle conjecture peut on émettre ?
2.Une preuve .
a,b,c désignent des nombre relatifs avec b ( = barré ) 0 et c ( = barré ) 0 tels que a=b+c
On pose x= a sur b et y= a sur c .
Démontrer la conjecture émise à la question 1 .
Donc voila même si c'est qu'une partie je vous en remercie de m'aider sur cette exo incompréhensible pour moi .
Bonne soirée .
-
LLind dernière édition par
Bonsoir

Multiplication des fractions :
a/b * c/d = ac / bd
(c'est-à-dire multiplication des numérateurs entre eux et des dénominateurs entre eux)Concernant l'addition des fractions :
Il faut impérativement mettre les deux fractions sur le MÊME dénominateur pour ensuite simplement additionner leurs numérateurs. Pour cela, il suffit de multiplier ou diviser la fraction.
2 / 3 + 5 / 6 = 22 / 32 + 5 / 6 = 4 / 6 + 5 / 6 = 9 / 6Je pense que ton cours t'apportera plus de précision.
« Un problème créé ne peut être résolu en réfléchissant de la même manière qu’il a été créé. »
« Rien n'est plus proche du vrai que le faux. »
**- A. Einstein * * ***
-
NNekoDown dernière édition par
Merci mais l' * est une division ?
-
NNekoDown dernière édition par
Et ps : Désolé mais peut tu me mettre la réponse soit du petit 1 ou petit 2 car la je ne comprends rien

-
LLind dernière édition par
Concernant la division ? Une fraction diviser par une fraction ? Il suffit de multiplier le numérateur par l'inverse du dénominateur :
(5/2)/(3/4) = 5 / 2 * 4 / 3 = 20 / 6 = 10 / 3
Je te résous a. x = 7/5 et y = 7/2 pour te donner un autre exemple.
Somme :
7/5 + 7/2 = 14/10 + 35/10 = 49/10Produit :
7/5 * 7/2 = 77 / 52 = 49/10A toi de continuer !
-
NNekoDown dernière édition par
Lind
Concernant la division ? Une fraction diviser par une fraction ? Il suffit de multiplier le numérateur par l'inverse du numérateur :(5/2)/(3/4) = 5 / 2 * 4 / 3 = 20 / 6 = 10 / 3
Je te résous a. x = 7/5 et y = 7/2 pour te donner un autre exemple.
Somme :
7/5 + 7/2 = 14/10 + 35/10 = 49/10Produit :
7/5 * 7/2 = 77 / 52 = 49/10Merci beaucoup je reposte en cas de problème

A toi de continuer !
-
NNekoDown dernière édition par
Juste une question pour la somme pourquoi 14/10 et 35/10 ?
-
LLind dernière édition par
Car pour réaliser l'addition de deux fractions il est impératif que ces deux fractions soient sur le même dénominateur.
Or, 7/5 et 7/2 diffèrent au niveau du numérateur, il faut donc y trouver un diviseur commun et 10 en est un bon exemple. Pour mettre les deux fractions sur un dénominateur égale à 10, j'au multiplié la première fraction, 7/5, par 2 (donnant alors 14/10) et la deuxième fraction par 5 (donnant alors 35/10).Ensuite, il ne me reste qu'à additionner les numérateurs : 14/10 + 35/10 = 49/10.
Il est interdit d'additionner des fractions qui ne sont pas sur le même dénominateur.
« Un problème créé ne peut être résolu en réfléchissant de la même manière qu’il a été créé. »
« Rien n'est plus proche du vrai que le faux. »
**- A. Einstein * * ***
-
LLind dernière édition par
Addition des fractions :
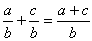
Multiplication des fractions :
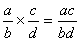
« Un problème créé ne peut être résolu en réfléchissant de la même manière qu’il a été créé. »
« Rien n'est plus proche du vrai que le faux. »
**- A. Einstein * * ***
-
NNekoDown dernière édition par
Merci beaucoup

-
LLind dernière édition par
Je t'en prie.
« Un problème créé ne peut être résolu en réfléchissant de la même manière qu’il a été créé. »
« Rien n'est plus proche du vrai que le faux. »
**- A. Einstein * * ***
-
NNekoDown dernière édition par
Le * c'est le signe division ?
-
LLind dernière édition par
Non, multiplication.
« Un problème créé ne peut être résolu en réfléchissant de la même manière qu’il a été créé. »
« Rien n'est plus proche du vrai que le faux. »
**- A. Einstein * * ***
-
NNekoDown dernière édition par
Ok merci bonne soirée à toi

-
LLind dernière édition par
Bonne soirée

« Un problème créé ne peut être résolu en réfléchissant de la même manière qu’il a été créé. »
« Rien n'est plus proche du vrai que le faux. »
**- A. Einstein * * ***