fonctions polynomes en économie

bonjour j'aurais besoin d'aide pour mon d.m
j'ai réussi les questions en gras mais je bloque sur le reste pouvez-vous m'aider ?

Compte tenu des conditions de production à un moment donné dans une chocolaterie, on modélise les variations des coûts de production (hors coûts fixes) du chocolat de façon suivante.
Pour une production de q en tonnes de chocolat, q inférieur à 1000, on estime que le coût en euros , noté C(q), est donné par:
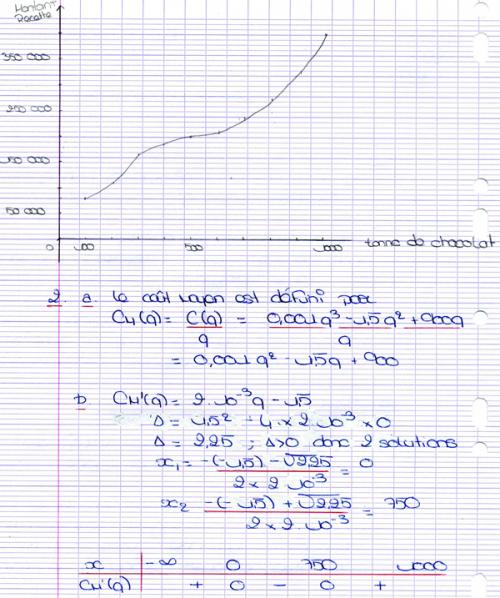
C(q)= 0.001q3-1.5q²+900q

1)étude de la fonction C

a) Calculer C'(q). Etudier le signe de C'(q) sur [0;1000]
b) En déduire que C est croissante sur [0;100]
c) Tracer la courbe représentative de la fonction C dans un repère orthogonal (unités graphiques: en abscisse, 1cm représnete 100t de chocolat; en ordonnées, 1cm représente 50000euros)

2)Etude de la fonction coût moyen C.m
On note C.M(q) le coût moyen en euros, d'une tonne de chocolat pour une production de s tonnes de chocolat (q est différent de 0)

a) Vérifier que C.M(q)=0.001q²-1.5q+900
b) Etudier les variations du coût moyen sur l'intervalle ]1;1000]
c) En déduire la quantité de q0 pour la quelle le coût moyen est minimal.
d) vérifier que la tangente à la courbe représentant C au point d'abscisse q0 passe par l'origine du repère.

Etude de la fonction coût marginal C.m
On note C.m(q) le coût marginal en euros, pour une production de q tonnes de chocolat.
Par la suite, on assimile le coût marginal à la dérivée du coût pour q appartient [0;1000] C.m(q)=C'(q)
a) Etudier les variations du coût marginal sur l'intervalle [0;1000]
b) Calculer C.m(q0) et vérifier que C.m(q0)=C.M(q0)
c) Tracer les courbes représentatives des focntions c.M et c.m dansu n repère orthogonal (unités graphiques: en abscisses, 1cm représente 100t de chocolat: en ordonnées, 1cm représente 200euros)

merci

Bonsoir,

Peut-on voir tes pistes de recherche ?

« Un problème créé ne peut être résolu en réfléchissant de la même manière qu’il a été créé. »

« Rien n'est plus proche du vrai que le faux. »

**-  A. Einstein         

* * ***

ou je vous scan ma recherche mais enfaite il ne me manque plus que la d de la partie 2 et la partie 3

$fichier math$ $fichier math$

Bonjour riridiabolik,

Un peu d'aide sur la méthode ...

1b) C'(q) > 0 donc la fonction C est strictement croissante (et non pas C')

2b) $C_M$ (q) = 0.001q² - 1.5q + 900

Tu as calculé C' $_M$ (q) = 0.002q - 1.5
il s'agit d'une fonction affine ... ton calcul d'un discriminant ne correspond à rien.
tu calcules simplement la valeur $q_0$ qui annule C' $_M$ puis tu dresses le tableau de variation de $C_M$

C'$$_M$(q_0$) = 0
0. $002q_0$ - 1.5 = 0
...
$q_0$ = ...

rappel : une fonction affine ax+b est du signe de a à droite de -b/a et du signe de -a à gauche de la même valeur

2c) $C_M$ est une parabole tournée vers le haut (coef de q² est positif), son mini correspond à $C$ _M $q_0$ ) que tu calcules.
Ou tu utilises simplement le tableau de variation.

2d) On te demande de trouver la tangente à la courbe C (et non pas de $C_M$ ) au point d'abscisse $q_0$ .

C(q) = 0.001q3 - 1.5q² + 900q

Application directe du cours : La tangente aura pour équation y = C' $q_0$ ) (q - $q_0$ ) + $C(q_0$ )

Une tangente est une droite, elle passe par l'origine si son équation est de la forme y = ax (ou si l'ordonnée à l'origine est nulle si tu préfères)

on assimile le coût marginal à la dérivée du coût C, donc :

Pour q ∈ [0;1000], $C_m$ (q) = C'(q) = 0.003q² -3q + 900 (calculé en 1a)

3a) $C_m$ (q) = 0.003q² -3q + 900

Tu calcules C' $_m$ (q) = ...
tu trouves une fonction affine, tu calcules la valeur de q qui l'annule et tu dresses le tableau de variation de $C_m$ (même méthode que 2b) ) (surtout ne calcule pas le discriminant de C' $_m$ ce n'est pas un polynôme du 2nd d° !)

La suite est du calcul et représentation ... bon courage.

je ne comprends pas ce que vous appelez discriminant ?

mon 2b est faux ?

pour le b c'est bon cela :

2 b. C.M'(q)=210-3q-1,5
C.M'(q)=0 => 210-3q-1,5=0 => 2*10-3q=1,5 => q=750
Si 1q <750, C.M'(q) <0 => CM(q) décroissante
Si q = 750, C.M'(750) = 0 => CM(750)=337,5
Si 750
0 => C.M(q) croissante

cela veut dire que le minimum est atteind en 337.5 ou en 750 ?

par contre je n'arrive pas a faire l'équation de la tangeante je vois la fomule mais je n'arrive pas a calculer

y=C'(750)(q-750)+C(750)

3a. cm'(q) = 0.006q-3

0.006q-3=0
0.006q=3
q=3/0.006
q= 500

et là je bloque pourriez vous m'aider cr je ne vois pas comment dresser un tableau de variation avec cela :s

b. pour cm(q0)=c'(q)
150=337.5

riridiabolik
pour le b c'est bon cela :

2 b. C.M'(q)=210-3q-1,5
C.M'(q)=0 => 210-3q-1,5=0 => 2*10-3q=1,5 => q=750
Si 1q <750, C.M'(q) <0 => CM(q) décroissante
Si q = 750, C.M'(750) = 0 => CM(750)=337,5
Si 750
0 => C.M(q) croissante

Oui

riridiabolik
cela veut dire que le minimum est atteind en 337.5 ou en 750 ?

Cela signifie que le coût moyen $C_M$ atteint un minimum de 337.5 € pour une quantité fabriquée de 750 tonnes de chocolat.

Merci je comprends mieux pourriezvous m'aider pour le reste ?

riridiabolik
par contre je n'arrive pas a faire l'équation de la tangeante je vois la fomule mais je n'arrive pas a calculer

y=C'(750)(q-750)+C(750)

Il n'y a pas de difficulté particulière, tu calcules :

C'(750) = 0.003 × 750² - 3 × 750 + 900

puis C(750) = 0.001 × $750^3$ - 1.5 × 750² + 900 × 750

Tu remplaces dans y=C'(750)(q-750)+C(750)

tu développes puis réduis pour la mettre sous la forme y = a q + b

si b=0, alors elle passe effectivement par l'origine.
tu la traces sur ton graphique pour vérifier que l'équation trouvée est correcte : elle doit être tangente à C et passée par O.

Citation
3a. cm'(q) = 0.006q-3

0.006q-3=0
0.006q=3
q=3/0.006
q= 500

et là je bloque pourriez vous m'aider cr je ne vois pas comment dresser un tableau de variation avec cela :s

oui C' $_m$ = 0.006 q -3
il s'agit d'une fonction affine de coefficient positif 0.006 qui s'annule effectivement en 500, donc :

pour q ∈ [0;500[ C' $_m$ < 0, la fonction coût marginal
$C_m$ est donc décroissante sur cet intervalle

pour q = 500, C' $_m$ = 0 et $C_m$ (500) = 150

pour q ∈ ]500;1000] C' $_m$ > 0, la fonction coût marginal $C_m$ est donc croissante sur cet intervalle

Tu peux dresser le tab de variation, d'accord ?

Citation
b. pour cm(q0)=c'(q)
150=337.5

Là je n'ai pas compris.

On a vu en 2d) que $q_0$ = 750 tonnes

tu calcules $C_m$ (q0) = $C_m$ (750) = 0.003 × 750² - 3 × 750 + 900

et tu vérifies simplement que tu trouves la même valeur que $C_M$ (750) = 337.5 trouvée en 2c)

... il faut essayer de ne pas se perdre dans les C(q) les CM(q) et les Cm(q) et leur dérivées.

ah ok
j'avoues que je me perds un peu dans tous les C lol

je récapitule

y=C'(750)(q-750)+C(750)
y= 337.5q-253125+253125
y= 337.5 q

j'ai donc bien une forme ax+b ou b=0

sur mon graphique je la trace comment j prend 0 et 337.5 en ordonné et je trace ?

3 b. cm(750) = 0.003 × 750² - 3 × 750 + 900
= 337.5

donc c'est bon cela coincide

3a.

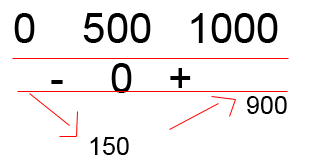
$fichier math$

pour la 3d. je rentre juste les deux formule dans ma calculette pour avoir les valeurs et tracer les courbes ?

Oui pour tout.

Citation
sur mon graphique je la trace comment j prend 0 et 337.5 en ordonné et je trace ?

La tangente d'équation y= 337.5 q est une droite, il te suffit pour la tracer de calculer 2 points ...

pour q=0 y=0 c'est l'origine que tu as déjà
et un autre par ex pour q=1000 y= 337 500

la tangente est la droite qui passe par ces 2 points, tu contrôles qu'elle est bien tangente à C (sur ton 1er graphique).

Citation
pour la 3d. je rentre juste les deux formule dans ma calculette pour avoir les valeurs et tracer les courbes ?
Oui un certain nombre de points dont les sommets pour tracer ces deux paraboles.

merci énormément pour tout

Travaille bien ce type d'exo ... très important pour la terminale.

à+