équation d'une tangente
-
Llaura92 dernière édition par
Bonjour, je suis en première ES et j'ai un exercice sur la tangente mais nous n'avons pas encore tellement vu ce chapitre. Pourriez vous m'aider à le résoudre svp ?
1°) soit f(x)= 3x/(x-1) défini sur ]1;+oo[
à l'aide de la calculatrice, calculer f '(a) , avec a=2
En déduire l'équation réduite de la tangente à la courbe Cf au point d'abscisse a
2°) Faire de même pour f(x)= -x² + x - 3 défini sur R pour a= -1
-
Zauctore dernière édition par

Salut
je veux bien, mais je ne sais pas ce qui a été vu en classe et derrière "à l'aide de la calculatrice" je ne sais trop que mettre...
je pense que tu ne sais pas encore déterminer une dérivée, mais s'agit-il de faire calculer le nombre dérivé par la machine elle-même ? s'agit-il d'utiliser un tableau de valeurs ? d'utiliser le grapheur et la position limite d'une sécante ?
c'est à toi de préciser de quelle manière vous avez abordé ce f '(a) en cours.
-
Llaura92 dernière édition par
il faut surement utilisé la formule y= f '(a) (x-a) + f(a)
-
Zauctore dernière édition par

merci je sais
ce n'est pas ce que je t'ai demandé.
tu as appris à calculer f '(a), oui ou non ? et comment ?
-
Llaura92 dernière édition par
pouvez vous m'expliquer comment calculer f '(a) ?
-
Zauctore dernière édition par

non (je le peux mais ne le veux pas - je ne vais pas (re ?)faire le cours)
je te demande de m'expliquer ce que tu as vu en classe à ce sujet pour adapter ma réponse à ton niveau (cf 12:54).
-
Llaura92 dernière édition par
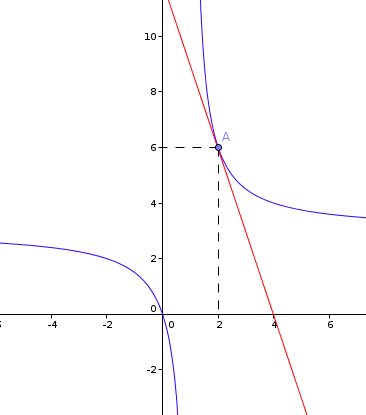
pour la réponse 1, l'équation de la tangente j'ai trouvé y= 6x - 6
-
Zauctore dernière édition par

pas du tout
tu as tracé la courbe ?
d'où sors-tu les coefficients ? (à part de l'équation dont tu as parlé plus haut)
(je continue à poser des questions bien que tu ne daignes pas y répondre)
-
Llaura92 dernière édition par
j'ai dis que f '(2)= 6 et que f(2)=6
donc y= f'(2) (x-2) + f(2)
=6(x-2) + 6
=6x - 12 +6
= 6x-6
-
Zauctore dernière édition par

justement f '(2) n'est pas égal à 6.
mais comme tu ne daignes toujours pas m'expliquer comment vous travaillez habituellement en classe avec ce nombre dérivé, je ne peux pas me hasarder à te donner des indications inadaptées à ton niveau ni à l'avancement des cours.