Exercice Géométrie - Cercle et diamètre
-
MMonizio dernière édition par
Bonjour,
J'ai besoin de votra aide pour résoudre le pb suivant. je dois rendre cette exercice pour le 26/04. dont voici l'énoncé
Dans la figure C et D sont deux points du cercle de centre 0 et de diamètre [AB]. (cf. image jointe)
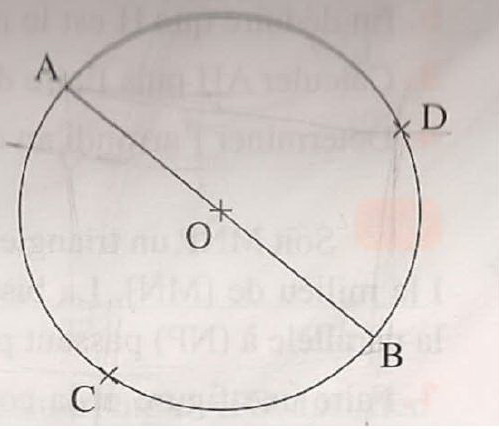
- Faire une telle figure en prenant: AB = 8 cm; AC = 6 cm et AD = 7,5 cm .
- Démontrer que ABC et ABD sont des triangles rectangles.
- La parallèle à (BD) passant par C coupe [AD] en K et la parallèle à (BC) passant par D coupe [AC] en L.
Prouver que les quatre points C, D, K et L sont sur un même cercle. Préciser son diamètre.
Merci d'avance de m'assister sur le point 3.
Monizio
-
IIron dernière édition par
Bonjour Monizio,
- justifie (à partir de la construction des points) que le triangle CLD est rectangle en L, puis
- justifie que le triangle CKD est rectangle en K
soit I milieu de [CD]
- Que peut-on dire du point L
- Que peut-on dire du point K
... à toi
-
MMonizio dernière édition par
Merci beaucoup pour ta réponse qui m'a bien aidée.

Donc, I est le centre du cercle sur lequel sont inscrits les point K, L, C et D.
J'ai pu justifier que les triangles CLD et CDK étaient rectangles grâce à la propriété suivante : Si un triangle est inscrit dans un cercle de diamètre l'un de ses côtés, alors ce triangle est rectangle.
Est-ce que c'est bon ?Merci.
-
MMonizio dernière édition par
Et en ce qui concerne le diamètre ?

-
IIron dernière édition par
Monizio
J'ai pu justifier que les triangles CLD et CDK étaient rectangles grâce à la propriété suivante : Si un triangle est inscrit dans un cercle de diamètre l'un de ses côtés, alors ce triangle est rectangle.
Est-ce que c'est bon ?Non, tant que tu n'as pas prouver que le triangle CLD est rectangle en L et que le triangle CKD est rectangle en K, tu ne peux pas affirmer qu'ils sont inscrits dans un cercle quelconque ...
Le début :
Par définition du point K, (CK) est parallèle à (BD)
Or (BD) ⊥((AD) d'après 2) et K est le point d'intersection des deux droitesPropriété : Si une droite (d1) est perpendiculaire à une droite (d2), toute droite parallèle à ... est aussi perpendiculaire à ...
-
MMonizio dernière édition par
Par définition du point K, (CK) est parallèle à (BD)
Or (BD) ⊥((AD) d'après 2) et K est le point d'intersection des deux droites. Donc si BD et CK sont parallèles, et que BD est perpendiculaire à AD, alors CK est aussi perpendiculaire à AD.
C'est bon ?
et ensuite la même chose pour le triangle CLD.
-
MMonizio dernière édition par
Voilà j'ai justifier, comment prouver maintenant que les points C, D, K et L sont inscrits dans un cercle I, soit le milieu de CD ?
-
IIron dernière édition par
Oui
Les deux triangles sont rectangles et ont même hypothénuse ...
-
MMonizio dernière édition par
Est-ce que ça prouve que les points C, D, K et L sont inscrits dans un même cercle ?

-
IIron dernière édition par
soit I milieu de [CD]
Le triangle CLD est rectangle en L et a pour hypothénuse [CD]. Le point L appartient donc au cercle C2C_2C2 de centre I et de diamètre [CD]
De même, le triangle CKD est rectangle en K et ...
De plus, il est évident que les points C et D appartiennent à C2C_2C2
En conclusion, les 4 points ...
-
MMonizio dernière édition par
Les 4 points sont inscrits sur le cercle C².
Merci!
-
MMonizio dernière édition par
Et la même chose pour le point K.
-
IIron dernière édition par
Oui, tout à fait ... mets tout à ta propre sauce, yapuka
-
MMonizio dernière édition par
Ok, merci beaucoup !