3. Angles au centre

Angles au centre

  • B

    Bonjour à tous!
    J'ai quelques problèmes
    La figure: Un cerle (C) ayant pour centre O et pour rayon R
    A , B, M appartiennent à (C)
    l'angle AMB= 30°
    le segment [NB] est un diamètre du cercle (C )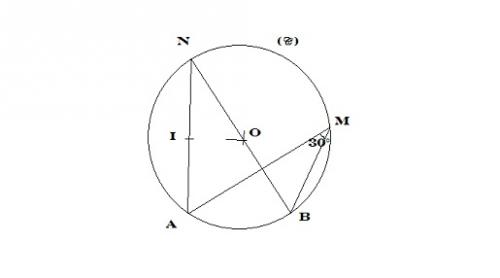

    fichier math
    1- Soit I le milieu , du segment [AN], montrer que les droites (OI) et (IN) sont perpendiculaires.
    Alors là j'ai mis que :Les droites (OI) et (IN) sont perpendiculaires car le point I représente le milieu de [NA] et O le milieu de [NB] est ce bon?

    2-a) Montrer que AB=2Rsin30° ce qui revient à dire à 3
    2-b) On admet que sin 30°=1/2
    et il faut exprimer la longueur AN en fonction de R (je ne comprends pas le sens de la phrase)
    Merci d'avance

    I 1 réponse
  • I

    Bonjour,

    Pour la 1) que peux-tu dire du triangle ABN inscrit dans C dont [AB] est un diamètre ?
    puis utilise la droite des milieux

    1. Que peux-tu dire des angles ANB et AMB ?
      Tu en déduis la valeur de l'angle ANB

    En utilisant la nature du triangle ABN (question 1)) et la valeur de l'angle ANB, déduis

    sin (ANB) = ... en remplaçant l'angle ANB par sa valeur.

    On te dit aussi que BN est un diamètre donc BN = ...

    Tu peux exprimer AB = ...

    1. Sachant que sin 30° = 1/2, tu peux exprimer AB en fonction de R

    Etant donné la nature particulière du triangle ABN, tu devrais pouvoir utiliser une propriété bien connue.

    B 1 réponse
  • B

    bonjour, tout d'abaord merci pour l'aide mais je n'ai pas compris
    pour la 1_ comme (BN) est un diamètre il faut utiliser le théorème des milieux ?
    dans le 2_ AMB est un angle inscrit au cercle et AND est-il un angle au centre? parceque si c'est cela il vaut le double de AMB soit 60°
    ABN est un triangle rectangle mais je ne comprends pas
    comment déduire sin(ANB) en remplaçant l'angle ANB par sa valeur ainsi que BN
    3- pour celle ci je n'ai pas trouvé la propriété mais j'ai juste trouvé que AB= R/2
    Merci d'avance.

    I 1 réponse
  • I

    si je réponds plus précisement, je vais faire ton exo, mais bon ...

    1. Le triangle ABN est inscrit dans le cercle C et son hypothénuse est un diamètre de C.
      Le triangle ABN est donc ... en ...

    donc les droites (AB) et (AN) sont ...

    La droite (IO) passe par I milieu de [AN] et par O milieu de [NB] car [NB] est un diamètre
    D'après la droite des milieux les droites (IO) et (AB) sont ...

    Si deux droites sont parallèles alors toute droite perpendiculiare à l'une est perpendiculaire à l'autre.

    Par conséquent les droites (OI) et (AN) sont ...
    Tu aboutis enfin à ton résultat.

    I 1 réponse
  • I

    bbt
    dans le 2_ AMB est un angle inscrit au cercle et
    AND est-il un angle au centre?parceque si c'est cela il vaut le double de AMB soit 60°
    ABN est un triangle rectangle mais je ne comprends pas
    comment déduire sin(ANB) en remplaçant l'angle ANB par sa valeur ainsi que BN

    un angle au centre serait un angle avec le point O "au milieu",

    1. Les deux angles AMB et ANB sont inscrits dans le cercle et interceptent le même arc de cercle AB.

    donc quelle égalité ? ... voir ton cours

    Dans un triangle rectangle : sin (angle) = coté opposé / hypoténuse

    utilise cela dans le triangle ABN pour exprimer sin (ANB)

    I 1 réponse
  • I

    bbt
    3- pour celle ci je n'ai pas trouvé la propriété mais j'ai juste trouvé que
    AB= R/2

    Bah ... et le bon "vieux" Pythagore alors !! (dans le triangle ABN)

    Citation
    AB= R/2
    Je n'ai pas trouvé ça, tu peux vérifier ?

Se connecter pour répondre