Brevet Métropole 29 juin 2010 - activités numériques

[Zauctore]

Bonjour

Voici les exercices de la partie numérique : le premier est très "à la mode" ces dernières années (niveau 4e) ; le second un peu plus intéressant mais guère difficile (niveau 5e-4e).

scan du sujet

1) a) En utilisant les parenthèses et en ne présentant pas les calculs comme un élève de 6e ce donne :

$(2\times -2+5)\times 5=1\times 5=5.$

b) Même chose :

$(3\times -2+5)\times 5=-1\times 5=-5.$

2) Par tâtonnement ou réflexion on voit que

$(2,5\times -2+5)\times 5=0\times 5=0.$
On peut aussi résoudre une équation :

$(x\times -2+5)\times 5=0$
au vu des nombres ce n'est guère utile.

3) L'expression proposée par Arthur donne

$(x-5{)}^2-x^2=x^2-10x+25-x^2=-10x+25=5(-2x+5).$
c'est bien l'expression du programme de calcul.

Remarque : j'ai développé avec une identité remarquable, ce qui n'est pas du tout obligatoire, en écrivant

$(x-5{)}^2=(x-5)(x-5)$
et en utilisant les "doubles-flèches".

[Zauctore]

scan du sujet

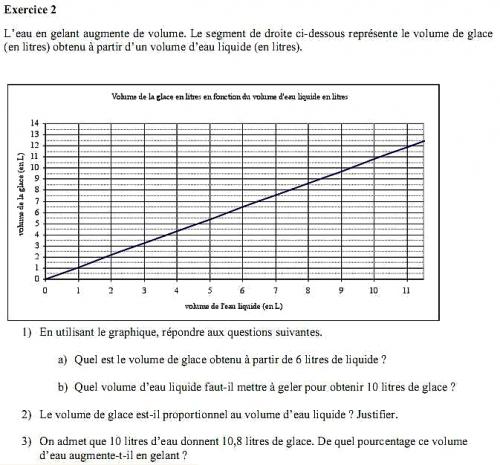
1) a) Par lecture graphique, on voit que l'image de 6 est 6,5. Le volume de glace obtenu à partir de 6 litres d'eau liquide est donc 6,5 litres.

b) Toujours par lecture graphique, on voit que l'antécédent de 10 est environ 9,3. A la précision permise par le graphique près, il faut mettre environ 9,3 litres d'eau liquide à geler pour former 10 litres de glace.

Remarque : pour ces deux questions, il était préférable de laisser des tracés apparents sur le graphique.

2) La représentation graphique étant une droite passant par l'origine du repère, on peut dire que le volume de glace est proportionnel au volume d'eau liquide.

3) Il suffit de trouver le nombre manquant dans la phrase :

10,8 par rapport à 10 sont comme ... par rapport à 100
La réponse est 108. Le volume de glace représente donc 108% du volume de l'eau : l'augmentation en volume est donc de 8%.

On pouvait aussi s'intéresser uniquement à l'accroissement en volume : 0,8 L d'augmentation pour 10 L, c'est comme 8 pour 100 (par proportionnalité).