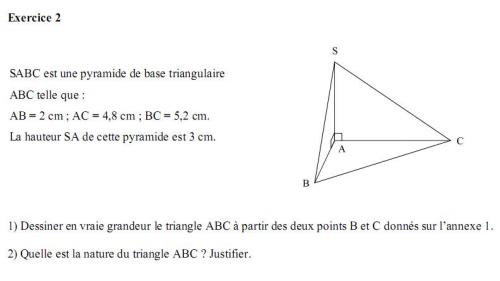
Brevet Métropole 29 juin 2010 - activités géométriques.
-
Zauctore dernière édition par

Sans difficulté, le premier exercice est du niveau 4e pour la deuxième question et 5e pour le reste.
scan du sujet
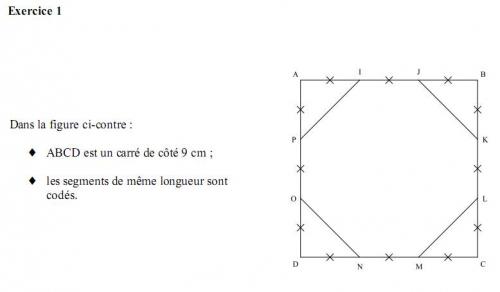

2) a) On se place dans le triangle BJK qui est rectangle en B. Le théorème de Pythagore permet d'écrire
jb2+bk2=jk2\small jb^2 + bk^2 = jk^2jb2+bk2=jk2
soit32+32=jk2\small 3^2 + 3^2 = jk^232+32=jk2
les codages montrant que BJ = BK = 9:3 = 3. D'oùjk=18=32≈4,2 cm.\small jk = \sqrt{18} = 3\sqrt2 \approx 4,2 \text{ cm}.jk=18=32≈4,2 cm.
2) b) Les côtés de l'octogone (c'est cette figure à 8 côtés obtenue en reliant IJKLMNOP, genre panneau de stop) ne sont pas tous égaux : certains mesurent 3 cm d'autres 4,2 cm. L'octogone n'est donc pas régulier.
2) c) L'octogone est obtenu en enlevant au carré les quatre petits triangles rectangles (identiques) des "coins". D'où l'aire de l'octogone :
92−4×3×32=81−18=63 cm2.\small 9^2 - 4 \times \frac{3 \times 3}2 = 81 - 18 = 63 \text{ cm}^2.92−4×23×3=81−18=63 cm2.
3) a)
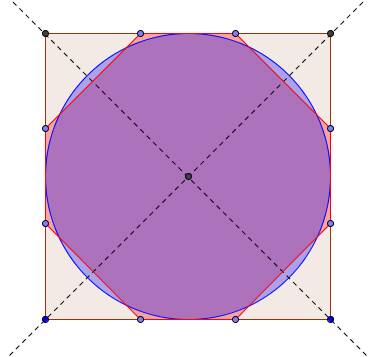
**3) b)**C'est vrai qu'on pourrait se laisser aller à imaginer que les portions de l'octogone situées en dehors du disque équivalent à celles du disque situées hors de l'octogone... c'est-à-dire imaginer que le disque et l'octogone ont sensiblement même aire... Mais le calcul montre que l'aire du disque est
π×r2=π×4,52≈63,6 cm2\small\pi \times r^2 = \pi \times 4,5^2\approx 63,6\text{ cm}^2π×r2=π×4,52≈63,6 cm2
L'aire du disque est donc légèrement supérieure à celle de l'octogone (il y a moins d'1% d'écart).Remarque : c'est une méthode égyptienne très ancienne pour approcher l'aire du disque.
-
Zauctore dernière édition par

scan du sujet