Limites, continuite

[marine88]

Bonjour, j'aimerais avoir votre aide en maths car je n'y comprends rien :S. Je voudrais qu'on m'explique simplement comment étudier les variations d'une fonction avec la dérivée mais aussi comment utiliser le théorème des valeurs intermédiaires et les limites. Si possible avec des exemples pour que je puisse comprendre l'application. Je sais que j'en demande beaucoup mais pour raisons personnelles je n'ai pu suivre les cours et je suis perdue. Je vous remercie d'avance

[Zauctore]

Bonjour et bienvenue !

Tout d'abord à propos des variations... prenons par exemple la fonction définie par

$f(x)=(1+x{)}^3-12x$
On veut savoir si elle est croissante, décroissante et sur quel intervalle ceci a lieu.

On calcule alors sa dérivée :

$f^{\prime }(x)=3(1+x{)}^2-12=3[(1+x{)}^2-4]=3(x-1)(x+3)$

On étudie le signe de cette expression (c'est pour cela que je l'ai factorisée) :
on voit que $f^{\prime }(x)$ est négatif si et seulement si $x\in ]-3,;,1[$.

C'est là qu'on utilise le théorème liant variations de $f$ et signe de la dérivée $f^{\prime }$.

On en déduit donc que la fonction f :

• est décroissante entre -3 et 1
• est croissante en dehors de ]-3 ; 1[.

Ceci est confirmé par la représentation graphique obtenue avec n'importe quel grapheur :

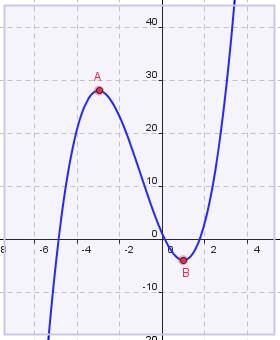
On retiendra que le signe de la dérivée donne le sens de variation de la fonction, n'est-ce pas !

[marine88]

merci pour cette réponse et personne d'autre concernant les limites et le TVI

[Zauctore]

Re.

Pour le tvi, commence par écrire l'énoncé qui t'a été donné en classe.

Pour ce qui est des limites, c'est un vaste sujet qui ne se traite pas en quelques posts. Quel genre de souci as-tu avec elles ?

[marine88]

En fait, pour les limites j'ai pu enfin comprendre l'essentiel mais pour le théorème des valeurs intermédiaires rien a faire j'ai des problèmes au moment ou il faut donner les intervalles