Arbre pondéré

[helene34]

Bonjour, voila j'ai un petit souci avec un arbre pondéré. Voici l'ennoncé

A et B sont deux événements associés à une epreuve aléatoire ?. A(barre) et B (barre) sont leurs événements contraires.
On considere l'arbre de probabilité ci dessous :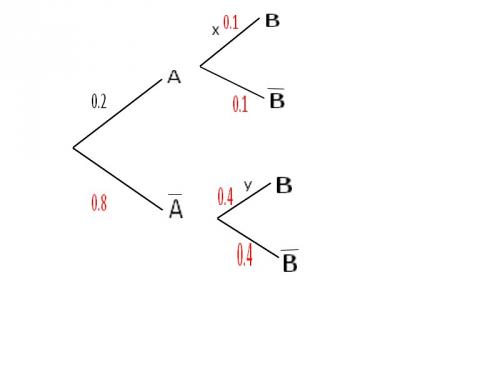

( Ce qui est ecrit en noir fait partie de l'enoncé, en rouge ce sont mes reponses).

1. a : Que représentent les nombres x et y ?
   b : Completer cet arbre

2. Exprimer p(B) en fonction de x et y.

3. Quelle relation doivent verifier x et y pour que A et B soient indépendants?

4. Exprimer pB(A) en fonction de x et y.

5. On suppose que y = 0.6
   Existe t il des valeurs de x pour lesquelles Pb(A) = Pa(B) ?

Alors voici mes reponses

1. a : x represente pA(B)
   y represente Pa barre (B)

b: cf arbre avec les reponses en rouge

2. p(B) = x+y

3. Pour que A et B soient indépendants, P ( x et y ) = P(A) x P(B)

4. Je n'ai aucune idée pour cette question

5. Je ne sais pas du tout.

Merci de votre aide.

[Zorro]

Bonjour,

Ton 1b est faux et les nombres en rouge ne collent pas ! Il faut que les probas de 2 évènements contraires donnent 1 comme somme !

Il faut mettre 1 - x et 1 - y sur les branches qui arrivent à $\bar{B}$

ET P(B) c'est aussi faux

[helene34]

Ok merci

Donc P(B)= 0.2x + 0.8(1-y) ?

[Zorro]

En utilisant les probabilités totales on a :

P(B) = P(A) * $P_A$(B) + P(Abarre) * $P_{Abarre}$(B)

il faut éviter les erreurs d'étourderie quand tu remplaces par les valeurs !

[helene34]

Ah oui j'ai confondu B et B barre
Donc P(B) = 0.2x + 0.8y

[Zorro]

oui

et Pour que A et B soient indépendants, il faut bien P ( A et B ) = P(A) x P(B)

Quelle équation cela te donne ?

[helene34]

P(A et B) = 0.2 x (0.2x + 0.8y)