[Dm] Les paraboles et les familles de droites associées

Bonjour
Et bien voilà mon petit souci: étant élève en 1ere STL, je suis tombé sur un prof de maths assez ... comment dire... "bête"? Insouciant? Frustré?
Je l'avais déjà l'année dernière, et son programme était le programme test de la 1ere S. Vous imaginerez aisément que mon année de mathématique de la seconde était catastrophique. Et cette année, je l'ai encore :mad: !
Résultat: je ne comprend rien à ses "cours" (si on peut appeler des exercices un cours) car je m'y perds facilement. Et je tiens à dire que pour toute la classe, la chose est la même...
Donc voilà, avant le week end, il nous a donné
un dm à faire pour mardi. J'ai planché dessus tout le week end, et je n'ai pas réussi à entrevoir quelque chose...
Je me tourne alors vers vous en espérant que vous puissez m'aider et me faire comprendre ce devoir

Voici l'exercice, réparti en 2 grosses parties. Voici tout d'abord quelques questions de la première partie.

Citation
"Sur une feuille F1 de papier millimétré, construire un repère ortho normé avec 2cm par unité sur chaque axe, puis tracer au compas le cercle ("oméga") de centre d'origine O et de rayon 2.

Justifiez brièvement que tout M (x;y) de ("oméga") vérifie x²+y²=4 (équation du cercle "oméga")

Soit m un nombre quelconque. A chaque valeur de m, on associe une droite (dm) unique dont une équation cartésienne est (m²-1)x+2my=2(m²+1). Les droites (dm) forment une famille.

*Construire avec soin en couleur sur la même feuille F1 les cinq droites d0, d-1, d+1, d-2, d+2
*Que constatez-vous quant à la position relative de chacune de ces quelques droites et de ("oméga")?
On vous propose dans la suite de cet exercice de démontrer ce constat ..."

Donc, je suis bloqué dès le début (d'autant plus que c'est la première fois que je vois des paraboles et les familles de droites!).

Je pense que le 1) constiste à mettre des chiffres à la place des lettres, alors je n'ai trouvé que ces solutions:
x²+y²=4
-> 0²+2²=4
Ou
-> 2²+0²=4

Dans le premier cas, x=0 et y=2. Dans le 2e, c'est l'inverse.
Suis-je dans la bonne voie?

Merci infiniement d'avance et j'espère à très vite!

Bonjour

Il n'y a pas de parabole pour le moment dans tout cela.

Pour ce qui est du cercle, tu connais le théorème de Pythagore - celui-là ne t'a pas été enseigné par ce professeur avec qui tu sembles avoir un "petit problème". Le fait que M soit sur le cercle fait de OM un rayon d'icelui, en conséquence de quoi en vertu du théorème sus-mentionné, tu peux calculer OM² au moyen de la formule de la distance en repère orthonormé

$OM^2 = (x_M - x_O)^2 + (y_M - y_O)^2$
La réponse en découle puisque $x_O = 0 = y_O$ .

On verra éventuellement le reste plus tard (avec moi ou une autre personne).

PS : En toute objectivité , les math de Première ne sont pas si compliquées.

Tout d'abord, merci d'être venu

Je ne comprend pas pourquoi on fait intervenir pythagore. Le seul théorème que j'ai appris de ce vénérable homme est celui du triangle et je ne savais pas qu'il pouvait s'appliquer aussi au cercle. Or ici, il n'est pas question de construction de triangle

Est-ce que la formule ci-dessus est un élément de réponse au 1) ? Car j'ai deviné que, sans le 1), on ne peut faire le 2) et ainsi tout l'exercice...
Quant aux paraboles, elles arrivent juste après
Merci!

PS: quelle chance !

Et les coordonnées ne font pas intervenir de triangle rectangle, peut-être ?

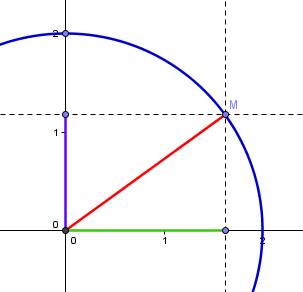
$fichier math$

Pythagore sert à prouver cette formule. C'est elle qui permet de répondre à la question 1.

Ah oui effectivement ^^ désolé :razz:
Mais alors, comment fait-on pour répondre à la question 1) et ainsi démontrer l'équation x²+y²=4?

Ce matin, j'ai cherché, et je ai trouvé:
Si x=2, alors y=0
-> 2²+0²=4

Mais si x=0, alors y=2
-> 0²+2²=4

On a deux solutions. Mais après ça, je ne comprend pas... :frowning2:

EDIT:
Oh, il faut juste mettre que
Om²= (xm-xo)²+(ym-yo)²
Pour que l'équation soit vérifiée? Pas besoin de faire intervenir des chiffres?

Oh et puis zut à la fin! Ce DM est sensé être sur les paraboles, alors, sautons (pour l'instant ) ces questions et passons aux choses sérieuses ^^!

Voici l'énoncé:

Citation
Soient les deux paraboles ...
(P1) d'équation y= t1(x) = x²+x-2 (P2) d'équation y= t2(x) = -x²+4x+3

*Mettre sous forme canonique chacun des deux trinômes t1-x) et t2(x)
*résoudre chacune des 3 équations ... t1(x)=0 t2(x)=0 t1(x)=t2(x)
*En déduire chacun des tableaux de variations complets des fonctions t1 et t2, en y faisant figurer les limites aux bornes (à l'infini), les extrema, ainsi que toutes les coordoné=nées des intersections des paraboles avec les deux axes et aussi entre elles.

Voilà où j'en suis:
1)* formes canoniques:
t1(x)= x²-x-2
=x²+2.1/2.x+1/4-1/4-2
=(x-1/2)²-9/4

t2(x)= -x²+4x+3
=-x²+2.2.x+2²+3-2²
(-x+2)²-1

(Je pense que le 2e est faux...)

C'est après que ça se complique pour moi. Le seul résultat que j'ai trouvé pour t1(x) est 7/4, mais c'est faux. Je pense, non, je suis sûr que c'est ma méthode qui est fausse:
(x+1/2)²-9/4 = 0
$s q r t$ (x+1/2)² =9/4
x+1/2=9/4
x=7/4

Merci d'avance pour votre réponse !

Ne sautons pas d'étape, merci.

I - Pour l'équation du cercle, Om²= (xm-xo)²+(ym-yo)² en introduisant évidemment les valeurs connues : O(0 ; 0), M(x ; y) et puis surtout le fait que OM = 2, rayon du cercle.

Cela donne OM² = (x-0)² + (y-0)² c'est-à-dire 2² = x² + y².

II - Ensuite, pour t1(x) = x²-x-2 = (x-1/2)²-9/4
je prétends que c'est de la forme a²-b², avec b = 3/2.
tu peux donc factorisersous la forme (a+b)(a-b).

III - Pour t2(x) = -x²+4x+3, j'aurais commencé par écrire -(x²-4x-3) pour ne m'intéresser qu'à x²-4x-3 finalement égal à (x-2)²-7 qui est lui-aussi de la forme a²-b², avec b=√7.

Merci beaucoup pour la réponse :D!
Concernant le I, j'ai compris, merci

Pour le II, est-ce que je suis obligé de le factoriser, même si ce n'est pas demandé?

Et pour le III, comment fait-on disparaître le signe négatif?

Hier, j'ai trouvé le premier tableau de variation (pour t1(x)).
Pour x=0, t1(x) =-2, et pour t1(x), on a deux solutions {-2;1}.
Ce qui donne une parabole passant par -2 d'abscisse, descendant à (-9/4;1/2) pour finalement remonter à 1 d'abscisse. L'allure de la courbe: ∪

Par contre je n'arrive pas à trouver les deux solutions pour t2(x)=0...

pour résoudre les équations, point de salut hors la factorisation !

Et bien merci à vous pour toutes ces réponses qui m'auront aidées à apercevoir la compréhension du cours ^^!