aidez-moi pour les asymptotes s'il vous plait
-
Vviirgiiniie dernière édition par
bonjour, serait-il possible que quelqu'un m'aide à comprendre avec beaucoup de simplicité les aymptotes?
-
Zauctore dernière édition par

Avec beaucoup de simplicité...
De façon générale et grossière, deux courbes sont *asymptotes *(à l'infini ou en une valeur "interdite") lorsqu'elles deviennent infiniment proches l'une de l'autre.
C'est donc un problème de "position-limite", en lien avec les limites proprement dites.
On étudie principalement les droites asymptotes, c'est-à-dire quand la courbe d'une fonction tend à ressembler de plus en plus à une droite. L'asymptote peut être horizontale (longeant l'axe des x), verticale (longeant l'axe des y) ou bien oblique...
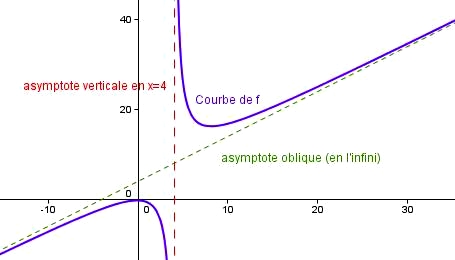
Dans la suite, je parlerai tout d'abord des asymptotes horizontales à l'infini, puis des asymptotes verticales en un point, pour finir avec les asymptotes obliques à l'infini.
[à suivre...]
-
Zauctore dernière édition par

Asymptotes horizontales à l'infini
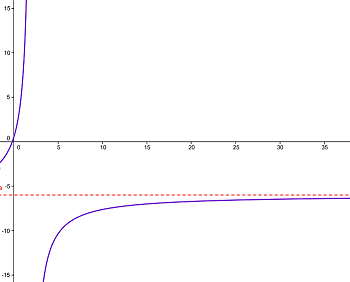
Rappelons déjà que l'équation d'une droite *horizontale *est de la forme y = *nombre fixé *: ainsi elle longe l'axe des abscisses parallèlement.Si la limite de f(x), lorsque x tend vers +∞, est égale à un certain nombre a, alors la droite d'équation y = a est asymptote horizontale à la courbe de f.
C'est par exemple de le cas avec f(x)=6x+12−xf(x) = \frac{6x+1}{2-x}f(x)=2−x6x+1.
En effet en forçant la factorisation par x, on voit que
f(x)=6x+12−x=x(6+1x)x(2x−1)=6+1x2x−1f(x) = \frac{6x+1}{2-x} = \frac{x\left(6+\frac1x\right)}{x\left(\frac2x-1\right)} = \frac{6+\frac1x}{\frac2x-1}f(x)=2−x6x+1=x(x2−1)x(6+x1)=x2−16+x1
donc à la limite, on alimx→+∞f(x)=limx→+∞6+1x2x−1=6−1=−6.\lim_{x \to + \infty} f(x) = \lim_{x \to + \infty} \frac{6+\frac1x}{\frac2x-1} = \frac6{-1}= -6.limx→+∞f(x)=limx→+∞x2−16+x1=−16=−6.
Illustration : lorsque les valeurs de x deviennent grandes, alors les valeurs de f(x) deviennent de plus en plus proches de -6.