Etude d'une fonction composée / fonction inverse

Bonjour.

J'ai un exercice de maths et j'aimerais savoir si mes réponses sont correctes.

$fichier math$

J'ai répondu:
1a) f(x)= g[u(x)]
On sait que g(x) > 0 donc U(x) est est tout ce qui est supérieur à 0, donc la fonction f est définie sur ]-infini ; 3[U]6;+infini[.

1b)

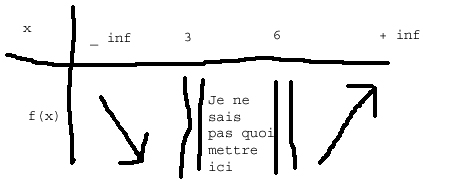
$fichier math$

2a) il faut que U soit différent de 0

2b) de - infini à 4 : croissant
de 4 à + infini: décroissant

2c)

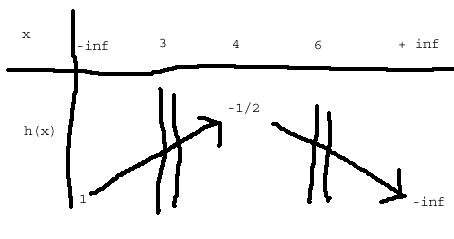
$fichier math$

Je me doute que j'ai au moins le 2C qui est faux, mais j'ai fait pour le mieux.

Merci d'avance si quelqu'un veut bien consacrer un peu de temps sur cet exercice.

Bonjour jaidumal

Citation
J'ai répondu:
1a) f(x)= g[u(x)]
On sait que g(x) > 0 donc U(x) est est tout ce qui est supérieur à 0, donc la fonction f est définie sur ]-infini ; 3[U]6;+infini[.

C'est plutôt mal exprimé
En fait, il faut simplement que u(x) > 0

1b) tu peux hachurer la zone [3;6], f n'y étant pas définie.

Pour justifier avec soin le sens de variation de f sur ]-∞;3[, il faut utiliser les règles sur le sens de variation des fonctions composées

sur ]-∞;3[, u est décroissante, g est ... donc f=gou est ...

Citation
2a) il faut que U soit différent de 0
Oui.

donc Dh = quoi ?

tu peux l'exprimer soit sous forme $mathbb{R}$ - {...} ou sous forme d'intervalles Dh = ]-∞;3[∪...

Citation
2b) de - infini à 4 : croissant
de 4 à + infini: décroissant
tu ne peux pas dire que h est croissante sur ]-∞;4[ car elle n'est pas définie en 3.

Il faut faire la même chose sur chaque intervalle qui compose son ensemble de définition.

idem en 6 bien sûr ...

2c) Ton tableau de variation n'est pas correct. Tes flèches ne peuvent pas traverser des valeurs interdites.

Exprime clairement Dh = ]-∞;3[∪...

ensuite ta méthode qui est correcte te conduira au bon résultat.

Merci beaucoup pour ces réponses.

1b) sur ]-inf ; 3 [ u est décroissante, g est croissante donc f= gou est décroissante.

2a) ...donc Dh = ]-inf ;3[U]6; +inf[

2b) sur: ]-inf ;3[ : croissant
sur ]3:4] : croissant
sur [4;6[ : décroissant
sur ]6;+inf[ : décroissant

2c)

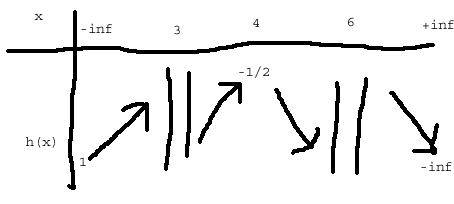
$fichier math$

Ce coup-ci, j'espère que c'est juste.
Encore merci.

Citation
1b) sur ]-inf ; 3 [ u est décroissante, g est croissante donc f= gou est décroissante.
Tu as de la chance que g est toujours croissante sur son ensemble de définition.

Sur ]-∞ ; 3 [, u est décroissante
et a valeur dans ] 0 ; 1 [
Sur ] 0 ; 1 [,g est croissante
donc f = gou est décroissante.

Citation
2a) ...donc Dh = ]-inf ;3[U]6; +inf[
Non, il faut juste éliminer les valeurs qui annulent u, cad 3 et 6.

Dh = $mathbb{R}$ -{ 3 ; 6 } soit
Dh = ]-∞;3[ U ]3;6[ U ]6;+∞[

Citation
2b) sur: ]-inf ;3[ : croissant
sur ]3:4] : croissant
sur [4;6[ : décroissant
sur ]6;+inf[ : décroissant

Les intervalles d"étude sont corrects, les sens de variation aussi.

pour les justifier, il faut présenter la fonction h comme la composée de la fonction u et la fonction inverse. La fonction inverse étant décroissante sur ]-∞;0[ ∪ ]0;+∞[

2c)

Juste une erreur dans ton tableau de variation :

En +∞, la fonction u tend vers +∞
Donc, en +∞, la fonction 1/u tend vers ... ?

ex 1/2000000 = un gros chiffre ou pas ?

Merci beaucoup!

Donc pour le 2C, en +∞ ce sera -∞

Bonne soirée à vous.

Non, pour le 2C, en +∞ ce sera 0

1 sur 5 millions, ça fait quelque chose proche de zéro, ok ?

bonne soirée

Et oui!

ça y est, j'ai compris merci