symétrie et démonstration

[gismon67]

bonjour voici le 2ème exercice de mon dm :

Dans cet exercice l'unité est le cm. On considère le triangle ABC tel que :
AB=4 ;AC=6;BC=3

1. Construire le triangle en vraie grandeur.

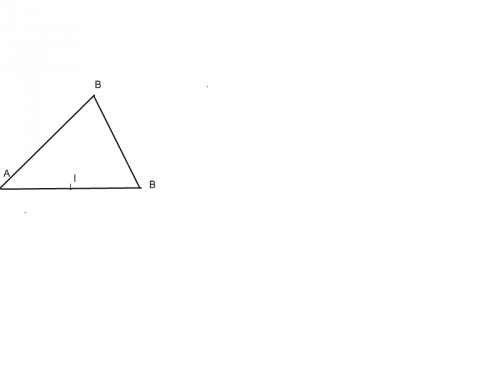
2. On désigne par I le milieu du segment [AC]. Sur la figure précédente construire le symétrique D du point B par rapport au point I.
   Quelle est la nature du quadrilatère ABCD? Justifier.(Ma figure est faites à peu près je sais pas trop utiliser paint)

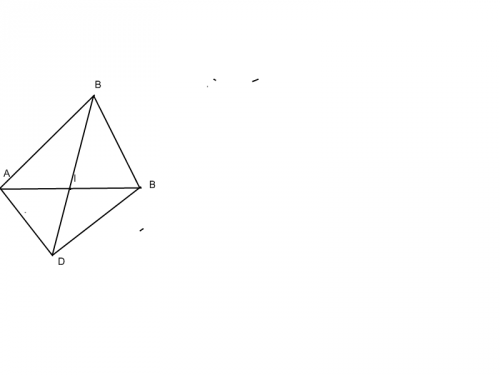
Si un quadrilatère à ses diagonales qui se coupent en leur milieu alors c'est un parallélogramme donc ABCD est un parallélogramme.

3. On désigne par F le symétrique de B par rapport à la droite (AC). Démontrer que les droites (DF) et (AC) sont parallèles.

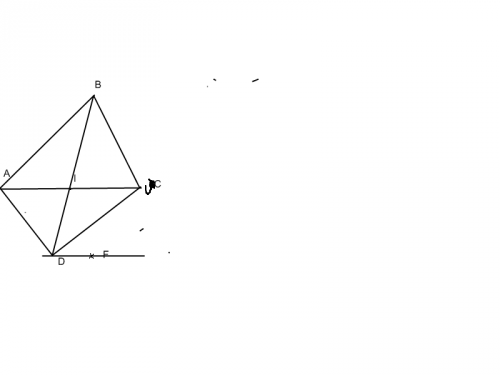
Et là je ne sais pas pourriez vous m'aider merci

[Iron]

Bonjour Gismon,

Citation
Si un quadrilatère à ses diagonales qui se coupent en leur milieu alors c'est un parallélogramme donc ABCD est un parallélogramme.
Oui. Précise peut-être tout de même que le point D est le symétrique du point B par rapport au point I. Par définition, I est donc milieu de [BD].

3. F le symétrique de B par rapport à la droite (AC).
   Soit J le point d'intersection de (BF) et (AC)

Que peux-tu dire de J pour [BF] ?

Dans le triangle DBF traversé (et pas n'importe comment) par la droite (IJ), utilise le théorème des ...

[gismon67]

Pour le 2) j'écris : D est le symétrique de B par rapport au point I,donc I est le mileu de [BD].
Si un quadrilatère à ses diagonales qui se coupent en leur milieu alors c'est un parallélogramme donc ABCD est un parallélogramme.

3)Je sais que : F est le symétrique du point B par rapport à la droite (AC), soit J le point d'intersection de (BF) et (AC) et le milieu de (BF) et I est le milieu de (BD)
or : dans un triangle, si une droite passe par les milieux de 2 côtés alors elle est parallèle au 3ème côté.
donc : (AC) // ( DF)

C'est ça ? merci

[Iron]

Citation
Pour le 2) j'écris : D est le symétrique de B par rapport au point I,donc I est le mileu de [BD].
Si un quadrilatère à ses diagonales qui se coupent en leur milieu alors c'est un parallélogramme donc ABCD est un parallélogramme.
Oui

Citation
3)Je sais que : F est le symétrique du point B par rapport à la droite (AC), soit J le point d'intersection de (BF) et (AC)
J est donc le milieu du
segment [BF
]
On sait aussi que I est le milieu de [BD]
or : dans un triangle, si une droite passe par les milieux de 2 côtés alors elle est parallèle au 3ème côté.
donc : (AC) // ( DF)

Attention, on parle tjrs du milieu d'un segment (pas d'une droite)

C'est bien.

[gismon67]

merci pour ton aide je reviendrai dans quelques temps pour donner la note obtenue

[Iron]

Je t'en prie.

à+

[gismon67]

Je n'ai pas oublié mais elle ne nous l'a pas encore rendu ce sera pour après les vacances je pense.
bonsoir