GEOMETRIE - cercle circonscrit et triangle rectangle

Bonjour à tous,

J'ai un problème de math, voici l'énoncé :

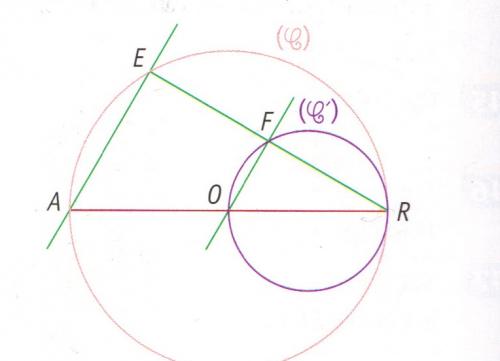
C est un cercle de centre O et de diamètre [AR]
C' est le cercle de diamètre [OR].
Le point E appartient au cercle C
La parallèle à la droite (AE) passant par le point O coupe la droite (ER) en F.

1°) Démontrer que le triangle AER est rectangle
2°) Démontrer que les droites (ER) et (OF) sont perpendiculaires
3°) En déduire que le point F appartient au cercle C'

REPONSES :
D'abord je fais la figure à main levée.
1°) Le triangle AER est inscrit dans le cercle de diamètre [AR]
Or, si u triangle est inscrit dans un cercle de diamètre d'un de ses côtés, alors ce triangle est rectangle et a pour hypotènuse ce côté.
Donc, le triangle AER est rectangle en E.

Voilà aprés j'ai besoin d'aide SVP
merci.

Bonjour,
Ta réponse est correcte.
2) Que sais-tu des droites (AE) et (ER) ?

la réponse 1 est complète ?
2) (AE) et (ER) sont deux côtés du triangle AER

La réponse 1 me semble complète. Corrige tout de même : hypoténuse ,
... ayant pour diamètre un de ses côtés ...
2) Je parle des droites, pas des segments.
Sachant que le triangle AER est rectangle en E, il en résulte que les droites (AE) et (ER) sont ...

perpendiculaires

Oui.
(AE) et (ER) sont perpendiculaires,
(AE) et (OF) sont parallèles,
or si deux droites sont parallèles, ....

si deux droites sont parallèles et si une troisième droite est perpendiculaire à l'une alors elle est perpendiculaire à l'autre

Donc ?

(ER) et (OF) sont perpendiculaires

Très bien.
3) Le triangle OFR ...

là je colle !

(ER) et (OF) sont perpendiculaires,
en Fpuisque c'est le point commun de ces deux droites :
Citation
La parallèle à la droite (AE) passant par le point O coupe la droite (ER) en F.Alors, le triangle OFR possède deux côtés perpendiculaires, c'est donc ...

(OF) milieu de [AC]
si dans un triangle une droite passe par le milieu d'un côté et est parallèle à un second côté alors elle passe par le milieu du 3ème côté ?

ok. c'est donc un triangle rectangle en F

Aucun rapport.
D'abord, le milieu d'un segment est un point, pas une droite !!
Ensuite, cela permettrait de démontrer que le point F est le milieu de [ER], rien à voir avec [AC].

Relis mon précédent message : le triangle OFR possède deux côtés perpendiculaires, c'est donc un triangle ...

je reprends depuis le début :
figure à main levée
1)1°) Le triangle AER est inscrit dans le cercle de diamètre [AR]
Or, si un triangle est inscrit dans un cercle de diamètre ayant pour diamètre un de ses côtés, alors ce triangle est rectangle et il admet ce diamètre pour hypoténuse.
Donc, le triangle AER est rectangle en E.
2) Sachant que le triangle AER est rectangle en E, il en résulte que les droites (AE) et (ER) sont perpendiculaires.

(AE) et (ER) sont perpendiculaires,
(AE) et (OF) sont parallèles,
or si deux droites sont parallèles et si une troisième droite est perpendiculaire à l'une alors elle est perpendiculaire à l'autre donc (ER) et (OF) sont perpendiculaires.
3) (ER) et (OF) sont perpendiculaires, en F puisque c'est le point commun de ces deux droites alors, le triangle OFR possède deux côtés perpendiculaires, c'est donc un triangle rectangle en F

Je pense être bien ?

enregistré depuis: oct. 2010
Messages: 13

Status: en ligne
(ER) et (OF) sont perpendiculaires

C'est bon.
Reste la suite : que sais-tu du cercle circonscrit à un triangle rectangle ?

le centre du cercle circonscrit à un triangle est le point de concours de ses médiatrices.

C'est vrai pour tous les triangles, mais ici, le triangle est rectangle : tu dois donc utiliser un théorème plus précis.

exact. donc si un triangle est rectangle alors le milieu de l'hypoténuse est le le centre de son cercle circonscrit.

Oui, on peut le dire autrement : le cercle circonscrit à un triangle rectangle admet pour diamètre l'hypoténuse de ce triangle rectangle.
Alors quel est le cercle circonscrit au triangle OFR ?

C'.

Oui.
Mais le cercle circonscrit à un triangle passe par tous les sommets de ce triangle, en particulier le point ?

le point F.

Terminé : F appartient au cercle C'.

ok. Merci beaucoup et au plaisir.

Talys

De rien.
A+

merci pour l'aide sa aide baucoup les autre persone en difficulté comme talys