Déterminer si une suite est bornée/ croissante/ décroissante/ convergente
-
PPierre86 dernière édition par Hind
Bonjour mes amis,
j'ai un QCM sur les suites réelles et je veux un aide à trouver les bonnes questions:- La suite (Un) définie par UnU_nUn=2-((n-1)/10) est :
*Bornée
*Croissante
*Décroissante
*Convergente
pour moi, j'ai choisi croissante( calculer UUU_{n+1}−Un-U_n−Un)
-
La suite(Un) définie par Un=(−1)n−1Un=(-1)^{n-1}Un=(−1)n−1/(n+1) est
*Borné
*Croissante,
*Décroissante
*Convergente
ma proposition est convergente(Lim tend vers 1/2) -
La suite (Un(U_n(Un) définie par UnU_nUn=cos(π/22/2^2/22)cos(π /23/2^3/23)…cos(π/2n/2^n/2n) est
*Bornée
*Croissante
*Décroissante
*Convergent
pour moi, je choisit décroissante -
Soit les suites (Un) et (Vn) définies par UnU_nUn=
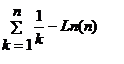 et VnV_nVn=
et VnV_nVn= 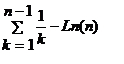 .Alors
.Alors
∗(Un*(U_n∗(Un) est décroissante
*(Vn) est croissante
*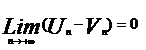
*Les suites (Un) et (Vn) sont adjacentes
vraiment j'ai pas pu trouver
Merci bcp

- La suite (Un) définie par UnU_nUn=2-((n-1)/10) est :