triangle rectangle, Pythagore, configuration papillon, Thalès
-
Ttemari.974 dernière édition par
Bonjour,
Quelqu'un peut m'aider à résoudre cet exercice s.v.p?
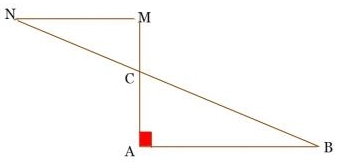
Enoncé
a) Le triangle ABC est rectangle en A ; on donne AB = 6 cm, BC = 10 cm.
a) Démontre que AC = 8 cm.
b) Sachant que CM = 2,56 cm et CN = 3,2 cm, explique pour quoi les droites (AB) et (MN) sont parallèles.Voilà mon travail.
a) pour démontrer on utilise pythagore.
Dans le triangle ABC rectangle en A.L'hypothénuse est [BC].On peut appliquer le théorème de Pythagore:
BC2BC^2BC2 = AC2AC^2AC2 + AB2AB^2AB2
10210^2102= ACACAC^2+62+6^2+62
100 =AC+36
AC2AC^2AC2= 100-36
AC2AC^2AC2= 64
AC= racine de 64
AC= 8
[AC] mesure 8 cm.b) on utilise la propriété :la réciproque de thalès
-
Zauctore dernière édition par

Bonjour
Ok pour a).
b) écris les rapports des côtés homologues et regarde s'ils sont égaux.
-
Ttemari.974 dernière édition par
les rapports sont NC/CB =MC/CA=MC/AB
C correct ?Oui ils sont égaux .
-
Zauctore dernière édition par

nn
du point de vue de la méthode, je dirais que tu t'y prends assez mal : ne pose pas d'emblée l'égalité des rapports, puisque tu ne sais si le théorème de Thalès va s'appliquer ou non.
ici il vaut mieux séparer les rapports pour déterminer leur valeur et ensuite les comparer (par exemple avec les produits en croix).
de plus, sache que tu n'as pas besoin de l'égalité avec le 3e rapport (transverse) pour appliquer la réciproque de Thalès.voici comment mieux présenter ton travail
d'une part, CA/CM = 8/2,56
d'autre part CB/CN = 10/3,2avec les produits en croix, on voit que 8×3,2 = 25,6 et 2,56×10 = 25,6.
les rapports sont bien égaux.
et tu peux maintenant invoquer la réciproque de Thalès pour conclure (avec une mention de l'ordre des points, pour faire au mieux).Edit : rectif d'une bourde initiale
-
Ttemari.974 dernière édition par
Merci , j'ai compris .
