Le ver de terre et les deux tourterelles sur leurs tours ...

Bonjour et bonne année à tout le monde ,

Je n'arrive pas à résoudre un problème dans un dm que j'ai à rendre pour lundi :

Deux tours hautes de 30m et de 40m sont distantes de 50m . Un ver de terre ( immobile ) est situé quelque part entre les deux tours . Deux tourterelles s'envolent en même temps du bord et d'en haut de chaque tour , elles volent à la même vitesse et arrivent en même temps sur le ver de terre.

Déterminer la position exacte du ver de terre entre les deux tours.

Je pense que c'est pythagore mais je n'arrive pas à résoudre ce problème ...

Bonjour

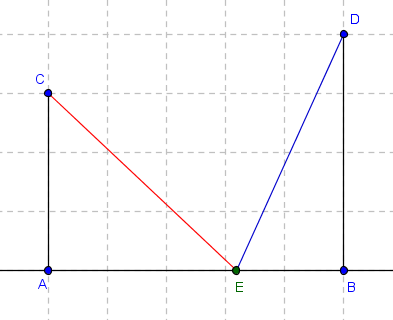
$fichier math$
La longueur rouge et la longueur bleue sont égales, d'après l'énoncé.
Applique Pythagore dans chaque triangle en utilisant ce fait.

Ok merci

Donc :CA² +AE² = CE²
30² +(50-x)²= CE² = 900 + 2500 - 100x +x² = 3400 - 100x + x²=CE²

DB² +EB² = ED²
40² + x² = ED² = 1600 + x² = ED²

Et après je bloque ...

En faite les périmètres des deux triangles sont égaux , non?

Sil-vous plait , expliquez-moi comment faire, étape par étape.

tu as posé x = EB, fort bien

tes calculs sont justes

utilise CE = ED pour simplifier le problème.

ce sont les hypoténuses (pas les périmètres) qui sont de la même longueur.

Ok merci , j'ai tout comprit maintenant, mais faut-il démontrer que les triangles sont rectangles?

Bonjour

L'énoncé lacunaire ne le précise pas, mais on peut supposer le sol parfaitement nivelé et horizontal, ainsi que les deux tours parfaitement verticales : on évite généralement les tours penchées comme celle de Pise !

ok , merci de m'avoir accordé tout ce temps.

Je t'en prie, c'est bien naturel.

A bientôt !