Application de la Dérivation

Bonjour Bonne Année !
Je ne comprend pas du tout l'exercice sur les dérivés si quelqu'un peu m'aider !
Merci d'avance.

Voila l'énoncé:

Dans un plan muni d'un repère orthogonal, on considère la courbe ci-dessous représentant une fonction définie et dérivable sur l'intervalle [-12 ; 12].
Les tangentes aux points d'abscisse -11 ; -5,5 ; -1 ; 4 ; 6,5 et 10 on été tracées.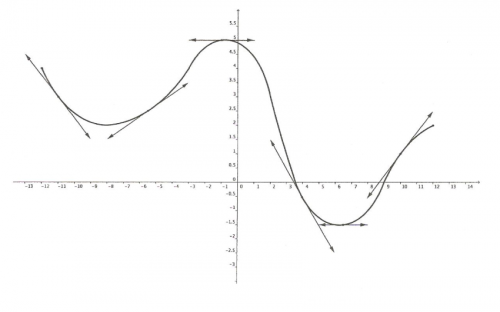

$fichier math$

I - Images de points et nombres dérivés.

a) Lire f(-11); f(-5,5); f(-1); f(4); f(6,5) et f(10)
b) Déterminer les coordonnées des points d'intersections de la courbe avec les axes du repère.
c) Lire f'(-11); f'(-5,5); f'(-1); f'(4); f'(6,5) et f'(10)

II - Équations de Tangentes.

a) Déterminer l'équation de la tangente au point d'abscisse -1
b) Déterminer l'équation de la tangente au point d'abscisse -5,5
c) Déterminer l'équation de la tangente au point d'abscisse 4
d) Déterminer l'équation de la tangente au point d'abscisse 6,5

III - Différents tableaux

a) Dresser le tableau de signes de la fonction f
b) Dresser le tableau de signes de la fonction f'

IV - Le signe d'une fonction, le signe de sa dérivée et le sens de variation de la fonction

a) Sur quels intervalles la fonction f est positive ? négative ?
b) Sur quels intervalles la fonction dérivée f' est positive ? négative ?
c) Déterminer le sens de variations de la fonction f en fonction de x.
d) Déterminer les extrema de la fonction f sur l'intervalle [-12 ; 0].
e) Déterminer les extrema de la fonction f sur l'intervalle [-3 , 12].
f) Pour quels abscisses, la fonction f atteint-elle ces extrema sur l'intervalle [-12 ; 0] ?
Sur [-3 ; 12] ?
Quel est le nombre dérivé correspondant à chacun de ces abscisses ?

Salut
Citation
I - Images de points et nombres dérivés.
a) Lire f(-11); f(-5,5); f(-1); f(4); f(6,5) et f(10)
Je t'assure que les 3e en 2010 savent le faire ; pas toi en 1re ?

Si je dis ça, c'est en réaction à ton petit texte introductif : Je ne comprend pas du tout l'exercice sur les dérivés si quelqu'un peu m'aider !

Mieux vaut dire ce que tu as fait, et ce que tu ne sais pas faire, car là tu t'es contenté de poster un sujet "brut".

Le I est simple mais le II déterminer l'équation de la tangente c'est plus compliqué et je ne comprend pas comment faire.

Au moins on sait par quoi commencer maintenant !
Citation
II - Équations de Tangentes.
a) Déterminer l'équation de la tangente au point d'abscisse -1

elle est clairement horizontale, non ?

→ équation y = ... (sans x)

Citation
b) Déterminer l'équation de la tangente au point d'abscisse -5,5
Lis le coefficient directeur et l'ordonnée à l'origine en prolongeant (ici c'est possible)

Rappel: le coefficient directeur est donné par

$\frac{y_1 - y_0}{x_1-x_0}$

a) si elle est horizontale alors y=0
vu que la pente est nul.

b) y= f'(a) × (x-a) + f(a)
= f'(2.5) × (x-(-5.5)) + f(-5.5)
= 2.5 × (-5.5x) + (-5.5)
= 13.75x + (-5.5)
= -19.75x

OU

y= f'(a) × (x-a) + f(a)
= f'(2.5) × (x-(-5.5)) + f(-5.5)
= 2.5 × x-(-5.5) + (-5.5)
= 2.5x - 11
= -8.5