Point d'intersection et droites d'un triangle

[talys]

Bonjour à tous,

Voici mon exercice :

A) Tracer un triangle et ses trois médianes.
Que constate-t-on ?
On constate que dans un triangle, ses trois médianes sont concourantes et se coupent en un même et seul point d'intersection.

B) TRACER UN TRIANGLE ABC :
La médiane issue de A coupe le segment [BC] en son milieu I.
La médiane issue de B coupe le segment [AC] en son milieu J.

On appelle G, le point d'intersection des deux médianes;
La droite 'CG) coupe le segment [AB] en K.
Le point H est le symétrique du point C par rapport au point G.

1. En considérant le triangle CBH, prouver que :
   (GI) parallèle à (BH)

On sait que dans le triangle CBH le point I est le milieu de [BC] et le point G est le milieu de [HC];
Or dans un triangle si une droite passe par les milieux de deux autres côtés alors elle est parallèle au troisième côte;
Donc (GI) parallèle à (BH).

2. En considérant le triangle CHA, prouver que :
   (GJ) parallèle à (HA).
   On sait que dans le triangle CHA le point G est le milieu de [HC] et le point J est le milieu de [AC];
   Or dans un triangle si une droite passe par les milieux de deux autres côtés alors elle est parallèle au troisième côte;
   Donc (GJ) parallèle à (HA).

3. En déduire que le quadrilatère AGBH est un parallèlogramme.
   On sait que (GJ) parallèle à (HB) et (GJ) parallèle à (HA).
   Or si un quadrilatère a ses côtés opposés parallèles alors c'est un parallèlogramme.
   Donc, le quadrilatère AGBH est un parallèlogramme.

a) Prouver que le point K est le milieu du segment [AB].
On sait que AGBH est un parallèlogramme, or un parallélogramme à ses côtés
diagonales qui se coupent en leur milieu.
Donc, K est le milieu du segment [AB] puisqu'il est le point d'intersection des diagonales du parallèlogramme AGBH.

b) Que reprèsente la droite (CG) pour le triangle ABC ? Justifier
Dans le triangle ABC, a droite (CG) reprèsente la troisième médiane issue de C coupant le [AB] en son milieu.

5. On vient de démontrer que :
   Dans un triangle, les trois médianes sont concourantes.

Merci de me corriger;
Talys.

[talys]

FIGURES

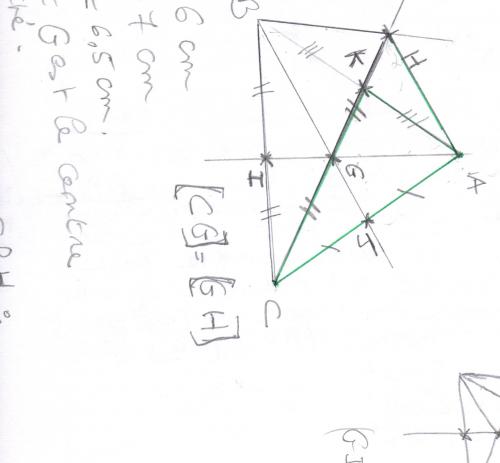
MERCI;

[mathtous]

Bonjour,
Tes raisonnements sont justes.
Seulement quelques points :
Citation
et le point G est le milieu de [HC]Justifie cela.
Citation
Or dans un triangle si une droite passe par les milieux de deux autres côtés alors elle est parallèle au troisième côtePourquoi "autres" ?
Si une droite passe par les milieux de deux des côtés ....
Citation
or un parallélogramme à ses côtés
diagonales qui se coupent en leur milieu.Ses diagonales, pas ses côtés diagonales.
Citation
Dans le triangle ABC, a droite (CG) reprèsente la troisième médiane issue de C coupant le [AB] en son milieu.Reprends cette phrase en commençant par ce que tu sais : la droite (CG) passe par le point K qui est ...

[talys]

Merci pour vos conseils et voici les modifications :

On sait que dans le triangle CBH le point I est le milieu de [BC] et le point G est le milieu de [HC] et G point d'intersection des médianes ,

La droite (CG) passe par le point K qui est le milieu du segment AB].

merci;

---

[mathtous]

Citation
On sait que dans le triangle CBH le point I est le milieu de [BC] et le point G est le milieu de [HC] et G point d'intersection des médianes ,Non : tu dois seulement justifier pourquoi G est le milieu de [HC] : comment est défini le point H dans l'énoncé ?
Mais tu ne sais pas encore que G est le point d'intersection des médianes ( seulement de deux d'entre elles ) ; il ne faut donc pas écrire la dernière partie de la phrase.

Citation
La droite (CG) passe par le point K qui est le milieu du segment AB].termine : donc c'est une médiane du triangle ABC ( par définition d'une médiane ).

[talys]

On nous précise dans l'énoncé :
On appelle G, le point d'intersection des deux médianes;
Le point H est le symétrique du point C par rapport au point G.

[mathtous]

Citation
On appelle G, le point d'intersection des deux médianes;
Oui, de deux médianes, pas des trois.
Si tu dis "des médianes ", cela sous-entend les trois.
Citation
Le point H est le symétrique du point C par rapport au point G.
Ce qui signifie que G est bien le milieu de [CH] : c'était la justification que je te demandais.

[talys]

ok, pour moi comme ç'est précisé des deux médianes il était évident
pour moi que ce n'était pas nécessaire de le préciser !

ok merci je m'en souviendrai.

Bonne soirée.

[mathtous]

Au revoir