Calcul de la hauteur d'un triangle à l'aide des relations trigonométriques

Bonjour,
J'ai un petit soucie sur un sujet. Le voici
Un pendule est constitué d'une bille suspendue au bout d'une ficelle d'un metre de long
Le pendule est en position d'equilibre lorsque la bille est en V. Il est écarté de sa position d'équilibre d'un angle de 30°, comme l'indique le figure, le bille est alors en P .
Donner la valeur exacte de la hauteur H, en mm, dont il s'est élevé .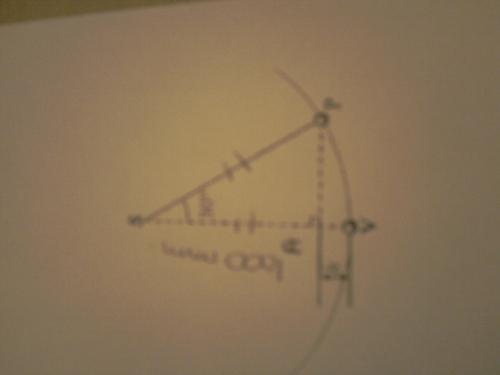

$fichier math$

Je pense a quelque chose comme Pythagore mais je ne sais pas comment procédé merci de m'aidez

Ok ce que tu cherches s'appelle la flèche. Ta figure est tournée d'une quart de tour à gauche.

Dans le triangle rectangle (où il y a l'angle de 30°) tu peux calculer 1000-h, si j'appelle h (en minuscule) la hauteur cherchée. Tu feras cela au moyen du cosinus, car tu connais l'hypoténuse 1000, le côté adjacent 1000-h et l'angle compris.

Je te rappelle qu'on a au choix :

adjacent = hypo × cos

cos = adjacent/hypo

hypo = adjacent/cos

selon les données du problème et ce qu'on veut calculer.

Oui mais le triangle rectangle est au dessus de la messure recherché donc cela pose un problème

cela ne pose aucun problème

si jamais tu trouves 1000-h tu en déduiras facilement h ; par exemple si 1000-h = 3, cela signifie que h = 997.

Euh je crois que je n'est pas vraiment tout compris

STP : "que je n'*ai *pas tout compris", *ai *du verbe avoir, et pas *est *du verbe être. Merci d'avance.

Tu te poses de faux problèmes : calcule, et tu verras bien où ça te mène.

Il faut déjà que tu trouves la longueur x dans la figure ci-dessous :

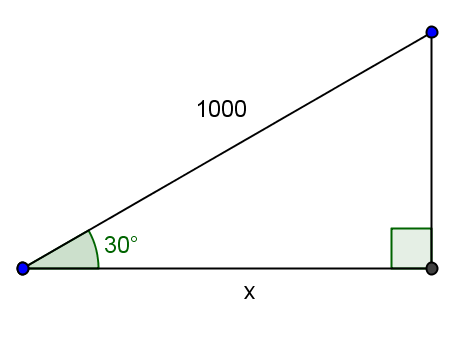
$fichier math$
Je t'ai proposé de le faire au moyen du cosinus. Valeur exacte de cos(30) = ... ?

cos 30°= x fois cos 30 ?

Attention : il faut faire l'effort d'appliquer correctement les formules

x = 1000 cos(30)

or cos(30) = √3/2

d'où la valeur exacte de x

Maintenant remarque sur ton dessin que x+h = 1000, et trouve h...

@+ je quitte

La formule de cosinus ne se fais pas comme ça.
cos= Adajacent/ hypotenuse

Ah Liloute...

si tu exerçais ta technique autant que ta répartie !

faut-il te guider à chaque ligne de calcul ? tu pars de la définition si tu veux, puis tu remplaces, tu fais une règle de trois et tu obtiens ce que j'ai écrit.

Si cela n'ai pas trop demander j'aimerais bien qu'on détails les calcul ensemble. Merci

ok

tu sais que par définition cos = adj / hypo n'est-ce pas

donc ici c'est cos(30) = x/1000

maintenant, en multipliant tout par 1000 pour chasser le dénominateur on arrive à 1000 cos(30) = x ce qui donne à la calculatrice x ≈ 866,025 en valeur approchée. c'est bon comme ça ?

malheureusement, l'énoncé demande une valeur exacte ; autrement dit il faut se servir de cos(30) = √3/2.

essaie voir.

Ah oui merci beaucoup d'avoir aussi bien détaillé

je t'en prie

est-ce que tu arriveras à calculer avec la valeur exacte ?

et sauras-tu en déduire h ?

Nan vraiment dédolé cette exercice est vraiment "bizar"je ne le comprend adsolument pas.