Dm de fonctions

J'ai un Dm a faire pour la rentré et je n'y arrive pas! :frowning2: Serait-il possible d'avoir de l'aide SVP.
Merci d'avance.

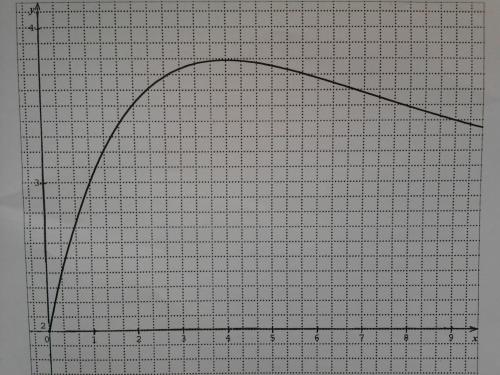
$fichier math$

1)On considère la fonction f définie sur [0 ; +∞[ par : f(x)= (ax+b) e^(-x/3)+3 ou a et b sont deux réels que l’on déterminera. La fonction f est représentée par une courbe C dans un repère orthogonal d’unités 1.5 cm en abscisse et 5 cm en ordonnées. La courbe C passe par le point A (0 ; 2). La fonction f admet un maximum de point d’abscisse 4.
a)Déterminer f’(x), ou f’ est la dérivée de f.
b)A l’aide des informations données sur la courbe C, déterminer les réels a et b.

2)Par la suite, la fonction f est définie sur [0 ; +∞[ par : f(x)=(x-1) e^(-x/3)+3 .
a)Déterminer la limite de f en +∞. En déduire l’existence d’une asymptote ∆ a C. Etudier la position relative par rapport a ∆.
b)Etudier le sens de variations de f et dresser son tableau de variations.
c)Tracer la droite ∆ et la courbe C

3)Les dépenses en téléphone d’une société sont données dans le tableau ci-dessous, pour 9 années consécutives. Xi est le rang de l’année et yl le montant de la dépense en k€ l’année xi.
xi 0 1 2 3 4 5 6 7 8
yl 1.97 3.02 3.49 3.71 3.80 3.76 3.65 3.55 3.50

a)Représenter ce nuage de point Mi (xi ;yl) dans le repère précédent.
b)Vérifier que pour chaque valeur xi, on a : /yi-f(xi)/≤0.1
c)Ce critère permet de dire que la fonction f est un modèle acceptable pour l’évolution des dépenses. Le responsable financier de la société affirme que, d’après ce modèle, on peut espérer retrouver une dépenses de téléphone inférieur a 3000€. Est-ce possible ? justifier la réponse.

Personne ne veut m'aider ? :frowning2: