Montrer qu'une fonction de référence est croissante et donner son tracé
-
Sstylo50 dernière édition par Hind
Bonjour , voici mon DM
Soit f est définie sur l'intervalle [0;+infini[ par :
f(x)= 3(racine carré de x) - 31- Montrer que la fonction f est strictement croissante sur l'intervalle
[ 0 ; +infini [ .2-Représenter graphiquement la fonction f dans un repère ( 0,I,J ) .
je n'arrive à répondre à aucune questions .
merci à ceux qui m'aideront ...
-
AAnonyme dernière édition par
- Il faut dériver f(x) et étudier la partie [0;+infini[
Au passage Racine(x) = x exposant 1/2
des fois ça peut servir ...Ok ?
-
mtschoon dernière édition par

Bonjour messinmaisouiet stylo50 ,
Vu que stylo50 poste en 1ES , en cette péride de l'année , je crains que les dérivées n'aient encore pas étaient abordées.
Vu le titre "Fonction de référence" , je me demande s'il ne s'agit pas d'utiliser directement le sens de variation connu de la fonction "racine carrée"
$\text{f(x)=3\sqrt x-3$
La fonction x -> √x est strictement croissante ( fonction de référence connue )
Vu que 3 est un nombre strictement positif , la multiplication par 3 conserve le sens de variation :
Donc , la fonction x -> 3√x est strictement croissante
Vu que -3 est une constante , ajouter -3 conserve le sens de variation :
Donc , la fonction x -> 3√x+(-3) , c'est à dire f , est strictement croissante
stylo50 va certainement nous dire ce qu'il connait ...
Evidemment , j'ignore si les raisonnements directs que j'indique lui conviennent...
Peut-être faut-il détailler :
Pour a et b positifs
Soit a < b , donc √a < √b ( car fonction racine carrée strictement croissante ) , donc 3√a < 3√b ( car 3 strictement positif ) , donc √a-3 < 3√b-3 , donc :
f(a) < f(b)
D'où la réponse souhaitée.
-
Sstylo50 dernière édition par
merci de m'avoir répondu
oui je n'ai pas encore fait les dérivées
c'est plutôt l'idée de mtschoon ( merci beaucoup )pour la 2 il faut que j'utilise la touche table sur la calculatrice ?
-
Ttcjose dernière édition par
f(x)=3x−3f(x)=3\sqrt{x}-3f(x)=3x−3
1- sur ]0,,,+∞[]0,,,+\infty[]0,,,+∞[, f′(x)=32xf'(x)=\dfrac{3}{2\sqrt{x}}f′(x)=2x3
qui est strictement positif. Par conséquent, f est strictement croissante sur [0,,,+∞[[0,,,+\infty[[0,,,+∞[
2- Voici la représentation graphique de la fonction f sur l'intervalle [0,,,5][0,,,5][0,,,5]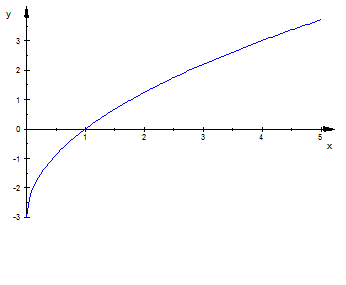
-
mtschoon dernière édition par

oui stylo50 , pour avoir des valeurs te permettant de tracer la courbe soigneusement , utilise la fonction TABLE de ta calculette , et bien sûr tu peux regarder la représentation graphique aussi sur ta calculette .
-
mtschoon dernière édition par

oui stylo50 , pour avoir des valeurs te permettant de tracer la courbe soigneusement , utilise la fonction TABLE de ta calculette , et bien sûr tu peux regarder la représentation graphique aussi sur ta calculette .
-
Sstylo50 dernière édition par
merci à tous pour votre aide
a+
