Partage d'un terrain en deux lots : Thalés
-
LLouise59180 dernière édition par
Monsieur Jean possède un terrain qu'il souhaite partager en deux lots de même aire.
Ce terrain a la forme d'un triangle ABC rectangle en A tel que : AB=40m et AC=100m.
L'aire du triangle ABC est égale à 2000 m2 et chaque lot devra donc avoir une aire de 1000 m2
Monsieur Jean décide de partager son terrain en un lot triangulaire AMN et en un lot ayant la forme d'un trapèze BMNC,comme indiqué sur la figure ci-dessous,
avec (MN) paralléle à (BC) .
On pose AM=x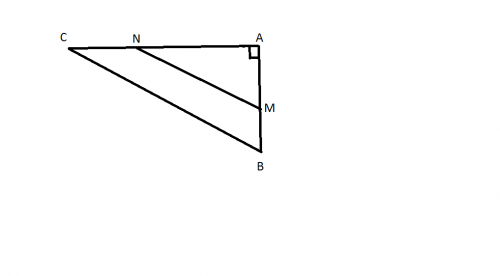
1ère question:
a) En utilisant la propriété de Thalés,Montrer que AN= 5sur2 x
b) Montrer que l'aire du triangle AMN est égale à 5sur4 x22ème question:
On note h la fonction qui,à un nombre x,associe l'aire du triangle AMN.
a)Recopier et compléter: h:x |->....
b)Quelle est la plus petite valeur possible pour x? Ou se trouve alors le point M ?
c)Quelle est la plus grande valeur possible pour x? Ou se trouve alors le point M ?
d)Calculer h(10),h(25)
-
Pptilargoun dernière édition par
1)a) AN/AC=AM/AB=NM/CB.
Et tu remplace les valeurs, après c'est résolutions d'équations. Mias il faut calculer le plus de côté possible avec l'aire qu'il te donne.