Etudier les limites à l'infini d'une fonction avec racine carrée
-
Jjugil dernière édition par Hind
Bonsoir;
Je vous contact suite à un problème de limite :
Il me faut étudier la limite de
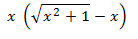 si elles existent en +infinie et -infinie.
si elles existent en +infinie et -infinie.Déjà comment prouver qu'elles existent ... ?
Ensuite en +infinie j'ai essayais la quantité conjuguée, j'ai essayé de factoriser mais rien à faire toujours formes indéterminée...
Pouvez vous m'aider svp ?
Merci
-
mtschoon dernière édition par

Bonsoir,
Pistes,
f est définie sur R
En -∞ , il n'y a pas d'indétermination.
Tu trouves directement -∞
En +∞ , il y a indétermination
Transforme avec la quantité conjuguée ( tu multiplies et divises par (sqrtx2+1+x)(sqrt{x^2+1}+x)(sqrtx2+1+x)
Après calculs , tu dois trouver 1/2
-
Jjugil dernière édition par
merci beaucoup ;
je viens de trouver

J'ai celle ci à résoudre mtn :
(1+(1/x))^x en 0+ ; +inf ; -inf
en 0+ je suis passé par la forme exponentielle et j'ai trouvé 1 ...
par contre en +inf et -inf je trouve 1... mais je devrais trouver e(1) ... Avez vous une piste ?
-
mtschoon dernière édition par

Piste
En +∞ ou -∞ : 1/x est voisin de 0
$(1+\frac{1}{x})^x=e^{xln(1+\frac{1}{x})$
ln(1+1x)∼1xln(1+\frac{1}{x}) \sim \frac{1}{x}ln(1+x1)∼x1
xln(1+1x)∼x1xxln(1+\frac{1}{x}) \sim x\frac{1}{x}xln(1+x1)∼xx1
xln(1+1x)∼1xln(1+\frac{1}{x}) \sim 1xln(1+x1)∼1
La limite cherchée est donc e1e^1e1 , c'est à dire e
-
Jjugil dernière édition par
merci c'est super rapide...
moi j'avais remarqué que lim ln(1+x)/x représente la dérivée en 0 de la fonction f: x---> ln(1+x) .... et f'(0)=1 ... d'ou la limite e...
merci
juste une dernier :
limite en 0 de (cos(3x)-1)/(sin(x²))
-
mtschoon dernière édition par

Au voisinage de 0 :
cos(3x)−1∼−(3x)22cos(3x)-1 \sim -\frac{(3x)^2}{2}cos(3x)−1∼−2(3x)2
sin(x2)∼x2sin(x^2) \sim x^2sin(x2)∼x2
Après calculs :
cos(3x)−1sin(x2)∼−92\frac{cos(3x)-1}{sin(x^2)} \sim -\frac{9}{2}sin(x2)cos(3x)−1∼−29
Limite : -9/2
Bonne nuit !