courbe paramétrée

[jugil]

Bonsoir;

Je dois etudier le support de la courbe paramétrée : branche infinie, allure etc...

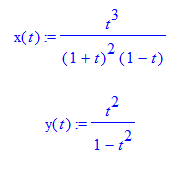
J'ai commencé par identifier l’ensemble de définition : R-{-1;1}

Ensuite ; j'ai conclut les limites suivantes:

lim |x(t)| = lim |y(t)| = +infinie au voisinage de -1 et 1 : donc il y aura des branches infinies à étudier au voisinage de ces points.

Étude en 1:

Je pose t=1+h et je fais un DL de x(t) et y(t)

x(1+h) = (1+h)^3 / (2+h)²(-h) et je trouve que c'est équivalent en 0 à -3/(10h)

y(1+h) = (1+h)²/(1-(1+h)²) et je trouve que (1-(1+h)²)=1-1-2h-h²-o(h^3) : mais c'est équivalent à -2h ou -h² en 0 ?

Ensuite comment conclure ?

Merci

[mtschoon]

Bonjour,

Je n'ai pas regardé tes calculs , mais si tu veux étudier la branche infinie pour t=1, le plus simple est de calculer la limite de y(t)/x(t) , lorsque t tend vers 1

Après simplification , sauf erreur :

$\frac{y(t)}{x(t)}=\frac{1+t}{t}$

La limite est donca=2

Ensuite , tu calcules y(t)-2x(t) et la limite lorsque t tend vers 1 ( tu dois trouver -∞ à gauche et +∞ à droite )

Il n'y a pas d'asymptote mais une branche parabolique de pente 2