le cercle trigonometrique
-
Sshrry dernière édition par
Bonjour
Dans un repere orthonorme du plan , le cercle triginometrique est le cercle ayant pour centre l'origine du repere et pour rayon l'unité.
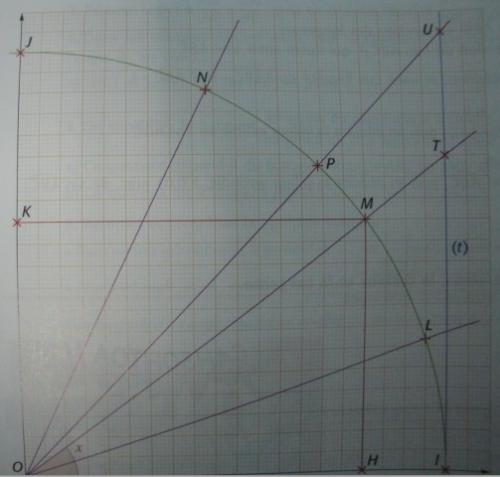
On a re presente ci-dessous le quart de cercke trigonometrique de centre O et de rayon 1 dm dans le repêre orthonorme (o,i,j) ce que signifie que (OI)perpendiculaire (OJ) et OI=OJ=1dm.Soit le point M (0.8;0.6).
La droite (t) est tangenrte au cercle en I et coupe la droite (OM)en T
on designe par x la mesure de l'angle IOM.Partie I
- cosinus d'un angle aigu
1)prouver que ; cos x = OH - que representer OH pour le point M?
a) en deduire une methode graphique pour determiner une valeur approchée du cosinus d'un angle .
b) quelle est , sur le graphique , la valeur de cos IOL ? - a) donner , avec la calculatrice une valeur arrondie de x au dixieme .
b) comparer le resultat avec la mesure du dessin .
Partie II
- justifier la nature de quadrilatezre OHMK
- prouver que ; sin x = HM=OK
- que represente OK pour le point M?
- a)En deduire une methode graphique pour determiner une valeur approchée du sinus d'un angle .*
b)quelle est ,sur le graphique , la valeur de sin ION?
5) a) a) donner , avec la calculatrice une valeur arrondie de x au dixieme .
b) comparer le resultat avec la mesure du dessinpartie III
1)justifier la nature du triangle IOT
2)proucer que ; tan x= IT
3)que represente IT pour le point T?
4)
a)En deduire une methode graphique pour determiner une valeur approchée de la tangenre d'un angle .
b) que lle est sur le graphique , la valeur de tan IOP?- a) donner , avec la calculatrice une valeur arrondie de x au dixieme .
b) comparer le resultat avec la mesure du dessin
- cosinus d'un angle aigu
-
mtschoon dernière édition par

Bonjour,
Tu n'as rien fait sur cet exercice ? ? ?
Je te le démarre mais on ne va pas faire tout ton exercice : ce n'est pas le but !
Partie I
cosx=ohom=oh1=oh\cos x=\frac{oh}{om}=\frac{oh}{1}=ohcosx=omoh=1oh=oh
- OH est l'abscisse de M
a) Tu mesures l'abscisse de M
b) Pour trouver graphiquement le cosinus de $\text{ \widehat{iol}$ , tu mesures l'abscisse de L
3)a) Tu prends ta calculette ( angles en degrés ).
Tu utilises l'inverse de la fonction cos
( regarde le fonctionnement de ta calculette .
sur ma calculette , je prends cos−1cos^{-1}cos−1(0.8) , mais ce n'est pas necessairement le même langage sur la tienne )Tu dois trouver x ≈36.87 °
Pour la partie II , c'est la même démarche pour le SINUS
Pour la partie III , c'est la même démarche pour la TANGENTE
-
Sshrry dernière édition par
- OH est l'abscisse de M la coordonnée du point M (0.8;0.6)
la coordonne du point H ( 0.8 ;0)
b) Pour trouver graphiquement le cosinus de , tu mesures l'abscisse de L
3)a)dans un cercle trigonometique on lit le cosinus sur l'axe x (abcisse)
b) le cosinus = cote adjacent /hypotenuse
OL=hypotenuse
OI=cote adjacent
la coordonnée du point L (0.95;2.5)
on sais que OI=1
0.95/1=0.95
donc le cosinus IOL=0.95a)cos -1(0.95 =18°
b) la mesure du dessin IOL = 18
les deux mesure sont identique.mais avec le cosinus on peut avoir plus de presision commen on a arrondie au dixieme .
- OH est l'abscisse de M la coordonnée du point M (0.8;0.6)
-
Sshrry dernière édition par lisaportail
Partie 2
- la nature du quadrilatere OHMK est rectangle
parce que la coordonnée K (0;0.6) M (0.8 ;0.6)
la coordonne H (0.8:0.6)O (0 ;0)
alors KM/ / HO MH perpendiculaire OH OK perpendiculaire OJ OI perpendiculaite OJ
il a trois angles droits - prouve que sinx= HM=OK
sinus = cote oppose/hypotenuse
sin IOM=MH/OM
OHMK est un rectangle
Un rectangle a ses côtés opposés 2 à 2 parallèles et de même mesure
o
Donc sinx=HM=OK
3) OK est le horizontale de M
le point M (0.8;0.6)
le point K(0;0.6)
4) dans un cercle trigonometrique de centre o et de rayon 1 on lit le sinus d'un angle sur l'axe y
( ordonnée)
b) sinus = cote oppose /hypotenuse
N1=0.9 OI=1
0.9/1=0.9
le sin ION= 0.9- a)sin.1(0.9=64
b) les deux mesure song identique.mais avec le sinus on peut avoir plus de presision comme on a arrondie au dixieme .
- la nature du quadrilatere OHMK est rectangle
-
Sshrry dernière édition par
Partie 3
OTI est un riangle rectangle
on sais que
La droite (t) est tangenrte au cercle en I et coupe la droite (OM)en TLe point T (1 ;0.65)
le point I (1 ;0)
la coordonnée du point M (0.8;0.6)
la coordonne du point H ( 0.8 ;0)2)prouver que tan x=IT
tangente = cote oppose /cote adjacent
tan IOT =IT /OT
Le point T (1 ;0.65)
0.65/1=0.65
tan x =IT3)IT est le cote oppose du angle OIT
4)tan IOP =1.05
5)tan-1(1.05=46
les deux mesure sont identique.mais avec la tangente on peut avoir plus de presision comme on a arrondie au dixieme
-
Sshrry dernière édition par
j' ai compris la 3 eme partie mais je ne suis pas sur de mon explicqtion
et je n'ai pas compris pour
que represente OH pour le point M
que represente OK pour le point M
-
Sshrry dernière édition par
complete la synthése suivant
je n'ai pas tous trouvéDans un repere …. (o;i;j) , les coordonnes d'un point M du cercle trigonometrique tel que IOM =x sont M (…;...) L' … du point d'intesection de (OM) avec la tangente en 1 au … est égale à tan …..
Dans un repere orthonorme (o;i;j) , les coordonnes d'un point M du cercle trigonometrique tel que IOM =x sont M (0.8…;0.6...) L' … du point d'intesection de (OM) avec la tangente en 1 au … est égale à tan …..
-
mtschoon dernière édition par

OH est l'abscisse de M
OK est l'ordonnée de MLes coordonnées de M sont (cosx, sinx )
Le point T a pour coordonnées (1, tanx)
-
Sshrry dernière édition par
que represente IT pour le point T?
Partie II
- justifier la nature de quadrilatere OHMK
Partie III
1)justifier la nature du triangle IOT
je peux explique comme ce que j'ai poste pour les reponses ci -dessus
- justifier la nature de quadrilatere OHMK
-
mtschoon dernière édition par

IT est l'ordonnée du point T
Tu peux justifier facilement que OHMK est un rectangle ( pense aux angles droits ) et que IOL et un triangle isocèle (OI=OL)
-
Sshrry dernière édition par
comment je complet la phrase
Dans un repere orthonorme (o;i;j) , les coordonnes d'un point M du cercle trigonometrique tel que IOM =x sont M (…;...) L' … du point d'intesection de (OM) avec la tangente en 1 au … est égale à tan …..
-
mtschoon dernière édition par

Si tu as compris les réponses précédentes , avec les éléments donnés , tu as tout ce qu'il faut pour compléter la phrase.
Fais une proposition et nous vérifierons.
-
Sshrry dernière édition par
Dans un repere orthonorme (o;i;j) , les coordonnes d'un point M du cercle trigonometrique tel que IOM =x sont M (cos(x)…;sin(x)...) L' (t )du point d'intesection de (OM) avec la tangente en 1 au …OI est égale à tan x(IOM).
-
mtschoon dernière édition par

****Le début est bon , mais pour le "L'..." c'est à revoir
Dans un repere orthonorme (o;i;j) , les coordonnes d'un point M du cercle trigonometrique tel que IOM =x sont M (cos(x);sin(x))
L'ordonnéedu point d'intesection de (OM) avec la tangente en I au cercle de rayon OIest égale à tan x .
Remarque : tu as mal lu le texte.
"La tangente en 1" ne veut rien dire : il s'agit de la tangente en I
-
Sshrry dernière édition par
b) comparer le resultat avec la mesure du dessin
je utilise le rapporteur pour repondre ?
-
Sshrry dernière édition par
- prouver que cos x=OH x = IOM
la trigonometriquer s'applique que dans un triangles rectangle
dans le triangle OMH
OM=1 dm MH=0.6dm OH=0.8dm
OM est le hypotenuse
pour prouver OMH est d'un triangle rectqngle on s'applique la reciproque de pythagore
1^2=1
0.6^=0.36
0.8^2=0.64
0.36+0.64=1
les points O H I sont alignes sur l'axe horizotal
donc MOH =MOI
cosinus = cote adjacent / hypotenuse
cos MOI = OH/OM
cos MOI =OH/1
cos MOI = OHdonc cos x =OH
je peux repondre comme ceci
ou il ya les expliquation plus simple
- prouver que cos x=OH x = IOM
-
Sshrry dernière édition par
ou je reponds
cos x = OH projete de M sur l'axe abscisses
est ce que c'est assez precis ?
-
mtschoon dernière édition par

Je ne vais pas rédiger ton exercice . Ce n'est pas le but.
Relis les réponses qui t'ont été données , comprends les et applique les.
Bon DM .