Applications

[thib083]

Bonjour, ne comprenant rien du tout à mon cour sur les fonctions d'une variable réelle et devant faire quelques exercices j'aurais besoin d'aide pour comprendre.

Donc on nous donne :
On considère la fonction f : x → √4-x² ( la racine englobe tout le 4-x²) dont la représentation graphique sur [ -2 ; +2 ] est :

je ne peux pas poster l'image, donc en effet elle est comprise en -2 et +2 et représente un demi cercle vers le haut.

On pose : I = [-2 ; +2] et J = [0 ; + 2]. Que pensez-vous des propositions suivantes ? :

Vrai Faux
a) f est une application de I vers J ..............................................................❐ ❐
b) f est une surjection de I sur J..................................................................❐ ❐
c) f est une injection de I dans J ................................................................❐ ❐
d) f est une bijection de I sur J ..................................................................❐ ❐

Tout d'abord je ne comprend pas le graphique, en quoi la racine de 4-x² donne ça ?
Après c 'est en effet une application et une surjection. Et ce n'est pas une injection et une bijection.
L'ensemble de départ est bien I donc -2 ; +2 ? et l arrivé J 0 ; +2 ?

• Si c'est ca c'est bien une surjection car J, ensemble d'arrivé d'arrivé d'arrivé à bien un antécédant de l'ensemble de départ I ? le +2 de J ayant pour antécédant le -2 de I ?

• Pour l'application : fonction dont l'ensemble de définition est égal à l'ensemble de départ, quel est l'ensemble de définition ?

• Pour injection je n'ai rien compris du tout

• Et ensuite pour la bijection je ne comprend pas trop non plus....

Merci d'avance pour votre aide.

[ptinoir_phiphi]

Salut

Si tu traces cette fonction sur ta calculatrice : tu dois trouver pour $c_f$ un demi cercle de rayon 2 qui se trouve au dessus de l'axe des ordonnées

Explicationspour calculer le domaine de définition de la fonction $f$ : $d_f$ :

Tu es sensé savoir qu'il faut que $4-x^2\ge 0$ pour que la fonction $f$ soit définie

Comme $4-x^2=(2-x)(2+x)$ , il faut faire une étude de signe pour trouver $d_f$

Conseil: relis ton cours ou va sur Wikipédia pour bien comprendre ce qu'est
une application de I dans J ,
une fonction surjective ou injective de I sur J
et enfin ce qu'est une bijection de I sur J

ps)
Dans cet exo on a : $d_f$ =I = [-2 ; +2]

et $f(d_f)$ =J = [0 ; + 2].

[mtschoon]

Bonjour,

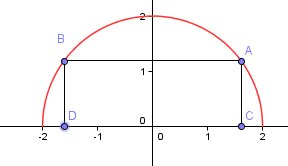
En ce qui concerne le graphique :

$y=\sqrt{4-x^2}$

Condition d'existence ( déjà vue ) : -2 ≤ x ≤ 2
necessairementy ≥ 0 ( pour que l'égalité soit possible )

En élévant au carré ( entre nombres positifs ) :

$y^2 =4-x^2 \longleftrightarrow x^2+y^2=4 \longleftrightarrow \fbox{(x-0)^2+(y-0)^2=2^2}$

Tu reconnais l'équation du cercle de centre O(0,0) et de rayon 2.

Vu que y ≥ 0 , tu obtiens le "demi-cercle supérieur "

Bien sûr , pour traiter ton exercice , tu aurais pu étudier les variations de la fonctiions f définie par $f(x)=\sqrt{4-x^2}$

CONSEQUENCES

f est une application de [-2,2] vers [0,2] car tout élément x de [-2,2] a une image y dans [0,2]

Pour les propriétés de cette application :

y=2 a un antécédent unique (x=0)
Tout y de [0,2[ a deux antécedents

Donc :

f et surjective car tout élément y de [0,2] a , au moins , un antécédent x dans [-2,2]

f n'est pas injectivecar tout élément y de [0,2] n'a pas ****, au plus, un antécédent x dans[-2,2]

Tu peux conclure quef n'est pas bijective car il faudrait à la fois qu'elle soit surjective et injective ( tout y de [0,2] devrait avoir un et un seul antécédent x dans [-2,2])