3. Le nombre d'or dans une suite de fractions

Le nombre d'or dans une suite de fractions

  • M

    Bonjour,

    Je fais mon DM dont la totalité du sujet porte sur le "nombre d'or", et je n'ai pas compris un de ses exercice...
    Voici l'énoncé :

    1. Calculer ((1+√5)/2)² et (1+√5)/2 +1. Comparer les deux nombres obtenus.
      Ma réponse : ((1+√5)/2)² = (3+√5)/2
      2.En déduire que (1+√5)/2 = 1+ 1/(1+√5)/2
    2. A partir de cette égalité, on peut en déduire que :
      (1+√5)/2 = 1+ 1/(1+√5)/2 = 1+ 1/1+(1+√5)/2 = 1+ 1/1+1/1+1/(1+√5)/2) = 1+1/1+1/1+1/1+1/(1+√5)/2)
      Ainsi on obtient une suite de logique de fractions définie à partir du nombre 1 à l'aide du raisonnement suivant : << pour trouver la fraction suivante, je prends l'inverse de la précédente et j'ajoute 1 >>.
      Cela donne F1= 1 ; F2= 1 + 1/1 ; F3= 1+1/ 1+1/1 ; F4= 1+1/1+1/1+1/1
      Ecrire F1,F2,F3,F5 sous forme d'une fraction irréductible et donner pour chacune d'elle une valeur décimale approchée à 10−310^{-3}10−3. Que remarque t-on ?

    A partir de la question trois j'ai du mal, quelqu'un peut m'aider s'il vous plaît ??

    M 1 réponse
  • M

    Bonjour,
    pose a = (1+√5)/2, et récrit les égalités données en utilisant a. (question 2 puis 3).

    M 1 réponse
  • M

    F2 =2 , f2= 1+1/2 =3/2 f3= 1+1/(3/2)= 5/3 f4= 1+1/(5/3) = 8/5

    M 1 réponse
  • M

    Attention, il y a un décalage dans tes indices :
    c'est f1 = 1, f2 = 2, f3 = 3/2, etc

    M 1 réponse
  • M

    F1 = 1
    F2= 3/2 ce qui donne ≈ 1,5 (à 10−310^{-3}10−3 près)
    F3 = 5/3 ≈ 1,67 (à 10−310^{-3}10−3 près)
    F4 = 8/5 ≈ 1,6 (à 10−310^{-3}10−3 près)

    Est-ce juste ??

    M 1 réponse
  • M

    F1, f2, et f4 sont des valeurs exactes : tu peux écrire "="
    f3 est une valeur approchée (tu dois écrire "≈") mais ce n'est qu'une valeur approchée à 10−210^{-2}10−2 près alors qu'on te demande à 10−310^{-3}10−3.

    M 1 réponse
  • M

    Que dois-je faire alors ?
    Je me suis trompé f1= 2
    et F5 = 13/ 8 ?

    Mais que dois-je remarquer ? Que ça se rapproche du nombre d'or ??

    M 1 réponse
  • M

    Il y a écrit que pour chacune d'elle doit être écrite sous forme de fractions irréductible..comment faire pour F1 je peux mettre F1 = 2/1 ?
    Et pour chacune d'entre elle je doit donner une valeur approchée à 10−310^{-3}10−3 comment faire pour F1,F2 et F4 alors ?

    M 1 réponse
  • M

    Citation
    Cela donne F1= 1 ; F2= 1 + 1/1 ; F3= 1+1/ 1+1/1 ; F4= 1+1/1+1/1+1/1Alors le décalage est dans l'énoncé ?
    Mais peu importe.
    En effet, ces fractions se rapprochent de plus en plus du nombre d'or.
    Tu peux t'en assurer en cherchant une valeur approchée de (1+√5)/2 avec une calculatrice.
    Pour les valeurs décimales, comme 8/5, tu peux écrire si tu veux 1,600 ( 3 chiffres après la virgule). Mais les valeurs approchées ne sont utiles que si les fractions ne sont pas décimales.
    Tu peux bien sûr écrire f2 = 2/1.

    P.S : n'envoie qu'un message à la fois.

    M 1 réponse
  • M

    Oui j'ai fait un décalage dans l'énoncé sans m'en rendre compte.
    Donc pour F1= 2/1 je ne peux donner de valeur approchée à 10−310^{-3}10−3 ?
    Et donc ça doit donner :
    F1= 1/2 = 2,000 (à 10−310^{-3}10−3 près)
    F2= 3/2 = 1,500 (à 10−310^{-3}10−3 près)
    F3= 5/3 ≈ 1,667 (à 10−310^{-3}10−3 près)
    F4= 8/5 = 1,600 (à 10−310^{-3}10−3 près)
    F5= 13/8 = 1,625 (à 10−310^{-3}10−3 près) ?

    P.S : Désolé j'avais oublié d'écrire l'autre partie..

    M 1 réponse
  • M

    Tu as fait une remarque correcte sur les valeurs (exactes ou approchées) des fractions. Tu peux aussi faire une remarque sur les fractions elles-mêmes : par exemple, quelle est la fraction F6 ?
    Observe bien tes précédentes fractions pour répondre.

    M 1 réponse
  • M

    F6= 1+1/13/8 = 1+1*8/13 =21/13 ≈ 1,615 (à 10−310^{-3}10−3 près) ?

    M 1 réponse
  • M

    Exact, mais tu n'avais plus besoin de faire les calculs.
    Observe : tu vois que le dénominateur de la nouvelle fraction est le numérateur de l'ancienne, et que le numérateur de la nouvelle est la somme du numérateur et du dénominateur de l'ancienne.
    Ainsi, la fraction suivant 21/13 sera (13+21)/21 = 34/21

    M 1 réponse
  • M

    Ah oui dois je le mettre dans la remarque ?

    M 1 réponse
  • M

    L'énoncé est peu explicite : "que remarque-t-on ?"
    Plein de choses ...
    Tu peux faire les deux remarques.

    M 1 réponse
  • M

    La totalité de mon DM porte sur le nombre d'or donc je pense que je vais juste dire que les valeurs ce rapprochent de celui-ci..
    En tous cas merci beaucoup !!!!!

    M 1 réponse
  • M

    De rien.
    Les fractions trouvées sont des approximations (pas toutes décimales) du nombre d'or.
    On peut dire plein de choses sur ce nombre.

    M 1 réponse
  • M

    Dans la partie 4 de l'énoncé on me demande: "A l'aide d'un tableur calculer les valeurs approchées à 10−1510^{-15}10−15 près (des 30 premières fractions de F1 à F30 ), que constate-t-on ?
    Je ne sais pas comment m'y prendre avec le tableur, pouvez-vous m'éclairer s'il vous plaît ?

    M 1 réponse
  • M

    Je n'ai pas l'habitude des tableurs et ne peux donc te venir en aide.
    Par contre; lis ce que Mtschoon t'écrit dans un autre de tes sujets : c'est la même chose sauf qu'au lieu de taper (1+racine(5))/2, tu tapes tes fractions (3/2, 8/5, etc).

    M 1 réponse
  • M

    Merci quand même !

    I 1 réponse
  • I

    Bjr,

    Comme l'a fait remarquer mtschoon, apparemment Excel ne gère pas la quinzième décimale (elles sont toutes à zéro).

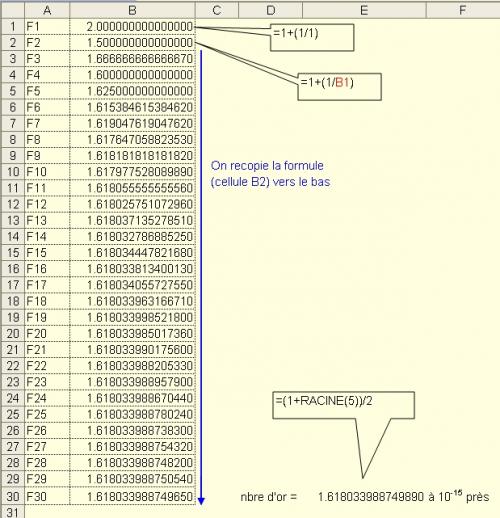
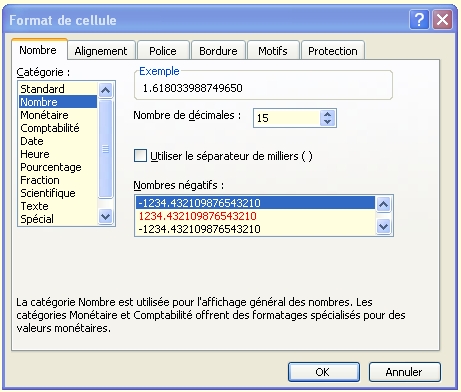
    fichier math

    Pour afficher 15 décimales, il faut modifier le "--> format --> celleule --> nombre" et afficher le nombre de décimales souhaitées.

    fichier math

    M 1 réponse
  • M

    Oui c'est ce que j'ai fait, merci !

Se connecter pour répondre