Représenter l'arbre de probabilité et calculer l'espérance

Bonjour a tous, j'ai un exercice sur les probabilités a faire. J'ai réussi a faire l'arbre de probabilité mais je bloque sur la suite ! Merci beaucoup a ceux qui pourront m'aider !

représenter l'arbre de probabilité associé a cette expérience aléatoire
on note R le rang de sortie de la boule rouge. Déterminez la loi de probabilité de la variable aléatoire R
calculer l'espérance mathématique de R

Merci d'avance !

Bonjour,

Il nous manque une bonne partie de l'énoncé pour qu'on puisse t'aider !!!! Je suis peut-être pas trop mauvaise en maths mais je suis assez nulle en divination et ma boule de cristal est en grève !

Ah oui mince j'ai complètement oublié de mettre le début de l'énoncé désolé : le début est donc : une urne contient trois boules blanches et une boule rouge. On tire au hasard une boule de l'urne jusqu'à obtenir une boule rouge.( Puis viens ce que j'ai posté !)
Merci pour ton information !

Il manque encore une précision ! Après chaque tirage d'une boule, on la remet ou pas dans l'urne ? Cela change un peu beaucoup la réponse et l'aide qu'on peut t'apporter !

On va envisager que c'est sans remise ..... Je t'envoie dans quelques secondes l'arbre que j'envisage.

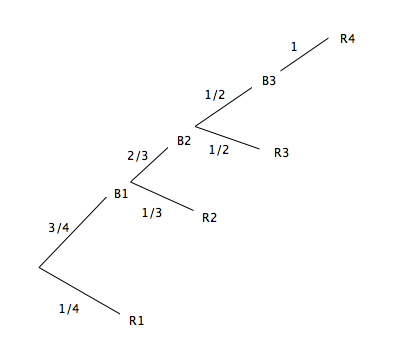
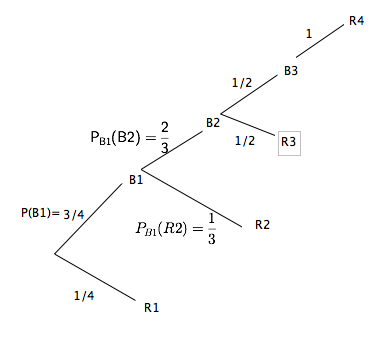
$fichier math$

B1 = "on tire une blanche au 1er tirage"
B2 = "on tire une blanche au 2ème tirage"
...
R1 = "on tire une rouge au 1er tirage"
R2 = "on tire une rouge au 2ème tirage"
....

La boule rouge peut sortir au 1er rang , au 2ème, ou au ......

Les valeurs prises par la variable R sont donc .......

Et

la proba que R vaille 1 est égale à ....
la proba que R vaille 2 est égale à ....

Ce sont ces probas qu'on te demande quand la question est ""Déterminez la loi de probabilité de la variable aléatoire R""

Je n'ai pas d'autres énonces plus précis désolé ! La loi de probabilité est donc : "puisqu'il il est possible de tomber sur 4 issues possibles alors chaque issue a une probabilite de 1/4" ??

Amis après je ne sais pas si il faut faire un calcul ou pas !

Il y a y a bien 4 cas possibles mais chacun n'a pas la même probabilité d'arriver....

La rouge sort au premier rang c'est P(R1) = 1/4

La rouge sort au deuxième rang c'est qu'on a eu une blanche au premier rang et une rouge au 2ème soit P(R2∩B1) = ....

Comprends tu la méthode et les calculs demandés ?

Pas vraiment ...

Il suffit d'appliquer la règle vue en cours : P(A∩B) = P(A) * $P_A$ (B)

La rouge sort au deuxième rang c'est qu'on a eu une blanche au premier rang et une rouge au 2ème soit

P(B1∩R2) =P(B1) * $P_{B1}$ (R2) = ....

Tu sais placer les probas conditionnelles sur l'arbre ?

$fichier math$