Calcul de la probabilité d'atteindre une zone lors d'un tir
-
KKN dernière édition par Hind
Bonjour, Je n'arrive pas du tout a commencer cet exercice,
Pierre est un tireur à la carabine qui ne manque jamais sa cible. Les quatre cercles ont pour rayons respectifs 1 cm, 2 cm, 3 cm et 4 cm. On admet que, quand Pierre tire, la probabilité qu'il atteigne une zone de la cible est égale au quotient de l'aire de cette zone par l'aire totale de la cible.
-
Quelle est l'aire exacte de la cible?
b Montrer que les aires des différentes parties de la cible en partant de la plus petites sont, en cm² πpipipi, 3πpipipi, 5πpipipi et 7πpipipi -
Pierre se présente et effectue un tir
Vérifier que la probabilité que Pierre atteigne la zone marquée 10 vaut 1/16
En déduire la probabilité que Pierre n'atteigne pas la zone marquée 10
3 Quelle est la probabilité que, lors d'un tir, Pierre atteigne la zone marquée 5 ou la zone marqué 3
-
-
KKN dernière édition par
Ou j'en suis :
- pi1²+pi2²+pi3²+pi4²
pi1+pi4+pi9+pi16
pi(1+4+9+16)
Je n'ai fait que la première question car je pense déjà que ce n'est pas la bonne réponse...
Merci de m'aider, svp.
- pi1²+pi2²+pi3²+pi4²
-
mtschoon dernière édition par

Bonjour,
Effectivement , ce n'est pas la bonne réponse.
Je suppose que tu as un schéma que tu ne nous donnes pas...
Vraisemblablement , la cible est le disque de rayon 4 donc : aire=∏ x 4² =16∏
Pour la suite , si tu ne donnes pas le schéma , précise quelles sont les zones marquées 10 , 5 , 3 . (* on peut l'imaginer mais il vaut mieux être sûr ..*.)
-
KKN dernière édition par
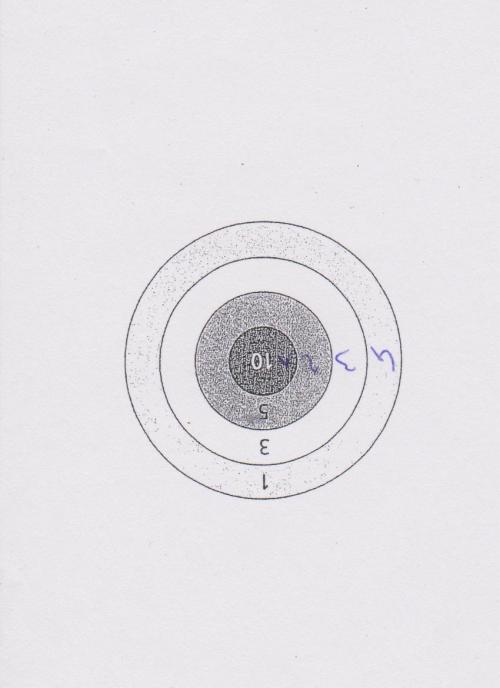
-
KKN dernière édition par
Elle est a l'envers je n'arrivais pas à la remettre droite.
Pour ma réponse je pensais qu'il fallait additionner l'ensemble des aires? (=chacuns des cercles)
-
mtschoon dernière édition par

La cible est le disque de rayon 4 : c'est l'intérieur du cercle de rayon 4donc l'aire est 16∏
Qu'as tu trouvé pour les questions suivantes ?