Montrer qu'une structure est un groupe par une loi donnée

Bonjour à tous, j'ai un exercice qui bloque, j'ai donc besoin de votre aide:
Soient les 4 fonctions de R* dans R*:
f1(x) = x, f2(x) = 1/x, f3x) = -x, f4(x) = -1/x
Montrer que G = { f1, f2, f3, f4 } est un groupe pour la loi o .
o : c'est le symbole de la composé

Bonjour,
Il y déjà de toute évidence une des fonctions qui est neutre (pour la composition).
En outre, la loi de composition est par nature ...?

JE ne comprend toujour pas

La loi de composition est par nature associative.
Calcule f1(f2(x)) ainsi que f2(f1(x)).

f1(f2(x)) = 1/x = f2(f1(x))

Conséquence : f2°f1 = f1°f2 = f2
Essaie avec f3 et f4 : tu verras bien que f1 est neutre pour la composition.
La composition étant associative, il te resteras alors à trouver l'élément symétrique de chacune des fonctions, et tu auras ton groupe.

si on continu avec f3 et f4 on a
f3(f4(x)) = 1/x = f4(f3(x)) = f2 .
mais je comprend pas quelque chose, vous dites que f1 est neutre pour la composition alors que si un element est neutre pour une loi alors pour tout element a de la loi ( * par exemple ) on a a*e = a . or ce n'est pas ce qu'on observe dans ce sujet

Citation
si on continu avec f3 et f4 on a
f3(f4(x)) = 1/x = f4(f3(x)) = f2 .Ce n'est pas exactement ce que je pensais en te disant de continuer: calcule f1°f3, f3°f1, f1°f4, f4°f1, et f1°f1.
Ainsi tu verras que f1 joue le rôle de ton "e".
Attention, pour une loi qui n'est pas commutative (ou dont on n'est pas sûr qu'elle le soit), il faut vérifier dans les deux sens : ae = a et aussi ea = a.

ok, c'est juste vous avez raison. donc il reste l'element symetrique pour chaque fonction. je prend un exemple si je suppose que f ' 1 est l'element symetreique de f1 alors
f 1'o f 1= f1 et j'essaie de trouvé l'element. est ca?

Citation
et j'essaie de trouvé l’élément. est ca?Tu as déjà le fait que le symétrique de f1 est f1 (normal, c'est l'élément neutre).
Tu essaies ensuite de trouver le symétrique de f2, de f3, de f4.

soit f ' 2 l'element symetrique de f2 alors
f ' 2 o f2 = f1
c'est à dire f ' 2 (1/x) = x. comment on resoud ca?

Citation
soit f ' 2 l'element symetrique de f2Tu ne peux pas écrire cela avant de l'avoir vérifié.
Calculons f2°f2(x) :
f2°f2(x) = 1/(1/x) = x
Donc f2°f2 = f1.
Tu fais pareil pour les autres.
Mais attention le symétrique d'un élément n'est pas forcément cet élément lui-même (quoi qu’ici ...)

Donc
f3 o f3 (x) = x
et f4 o f4 (x) = -1/-1/x = x donc les element symetriiques des fonctions sont elles memes

Tu peux conclure.
Si tu effectues tous les calculs (par exemple f2°f3), tu pourras dresser la table de ton groupe : est-il commutatif ?

Oui, on a affaire à un groupe abelien. lorsque je fais les calculs j'obtient
f2 o f3 = f3 o f2
f2 o f4 = f4 o f2
f3 o f4 = f4 o f3

Bonjour Mathtous et pierresimpore ,

Mathtous t'a donné toutes les indications utiles !

Je me permets un petit "plus".

Pierresimpore , lorsque tu rédigeras ton devoir , je te conseille de commencerpar faire la table de la loi o ( en faisant tous les calculs , bien sûr )

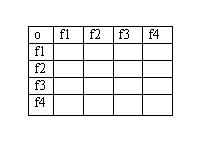
$fichier math$
En effet , pour que (E,o) puisse être un groupe , il faut d'abord que o soit interne dans E, c'est à dire que le composé de 2 éléments de E soit un élément de E

Ensuite , en t'aidant des conseils deMathtous et des valeurs trouvées dans la table , tu déduis les propriétés .

Bonne rédaction !