Déterminer si R est une fonction / application

[magy]

bonjour,
Voila mon probleme:
1)Soit E=F=R,et G={(x,y) appartenant a R2 | x2+y2<(ou egal)à1}
2)Quel est le domaine de définition de la relation R=(E,F,G)?Est-ce que R est une fonction?une application?
2)Memes questions si G={(x,y)2 appartenant à R2|x2+y2=1}

[mtschoon]

Bonjour,

Pour t'aider , il faudrait comprendre ce que tu as écrit...ce n'est pas mon cas. J'interprète ! ( *regarde ton cours , pour savoir si mon interprétation est bonne *)

Si E=F=R , je suppose que R représente l'ensemble de réels.
R=(E,F,G) est un non sens .
Peut-être que la relation se note r=(E,F,G)

Peut-être que x ∈E et y∈F et que G est le graphe de la relation .

Si c'est ça (?) , au 1) , G est le disque fermé de centre 0 et de rayon 1.
Fais un schéma pour plus de clarté .

-1 ≤ x ≤ 1 : l'ensemble de définition est [-1,1]

x²+y² ≤ 1 <=> y² ≤ 1-x² <=> $|y|\le \sqrt{1-x^2}$

Tout x de [-1 , 1] a une infinité d'images y

Donc ni fonction , ni application.

Raisonne de la même façon pour le 2) , en supposant que mon interprétation de ton énoncé soit bonne ( ce que j'ignore )

Mais... , au 2) , que veut dire ce "G={(x,y)2" ? ? ? Est-ce une faute de frappe ?

[magy]

l'interprétation est bonne!mais je comprens pas...

[mtschoon]

C'est déjà ça ...si l'interprétation est la bonne !

Précise ce que tu ne comprends pas.

[magy]

Pourquoi l'ensemble de définition c'est[-1 1] et tout le reste?

[mtschoon]

L'ensemble de définition est l'ensemble des valeurs que peut prendre x pour que y soit calculable.

$|y|\le \sqrt{1-x^2}$ Tu as bien compris ça , je suppose .

condition d'existence: 1-x² ≥ 0 <=> -x² ≥ -1 <=> x² ≤ 1 <=> -1≤x≤1

L'ensemble de définition est donc [-1,1]

Pour chaque valeur de x comprise entre -1 et +1 , tu cherches combien il peut y avoir de valeurs de y : içi, une infinité.

$|y|\le \sqrt{1-x^2}\leftrightarrow -\sqrt{1-x^2}\le y\le \sqrt{1-x^2}$

Pour avoir une application, tout x de [-1,1] devrait avoir une seule image y
Pour avoir une fonction, tout x de [-1,1] devrait avoir au plus une image y

Pour mieux comprendre , dessine le disque fermé de centre 0 et de rayon 1 ( qui correspond à x²+y²≤1)

[magy]

euh... d'abord:Pourquoi on |y| au lieu de y

[mtschoon]

$y^2\le 1-x^2$

En prenant la racine carrée de chaque membre ( positif ) :

$\sqrt{y^2}\le \sqrt{1-x^2}$

or , $\sqrt{y^2}=|y|$

Je détaille la raison :

Pour y ≥ 0 : $\sqrt{y^2}=y=|y|$
Pour y ≤ 0 :$\sqrt{y^2}=-y=|y|$

donc :

$\fbox{|y| \le \sqrt{1-x^2}}$

[mtschoon]

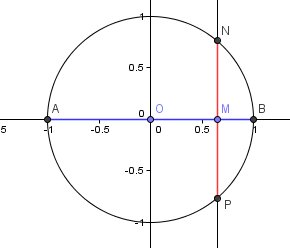
Pour faire l'interprétation ( et mieux comprendre ), tu peux utiliser cette figure :