Triangle équilatéral, racine carrée

Bonjour, j'ai commencé un exercice mais je n'arrive pas à le finir. J'espère que vous pourrez m'aider.
Voici l'énoncé ( je suis désolé, je n'ai pas pu ajouter les codages de la figure, donc je vais vous les énoncer)
Le triangle ABC ci-contre est équilatéral.

Calculer AH si a = 4 cm
Exprimez AH en fonction de a.

Codages : a=AB
BH=HC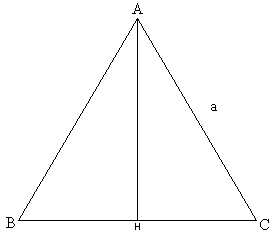

Ce que j'ai fait :

Dans HAC, rectangle en H, j'applique le théorème de Pythagore et j'ai :
AC²=HC²+AH²
AH²=AC²-HC²
= 4²-2²
= 16-4
= 12

AH = √12
= √3×4
= √3 × √2²
= 2√3

Voila c'est tout, je n'ai pas réussi la deuxième question....
Merci d'avance

Bonjour,
Attention : écris √(3×4) et non √3×4 : il y a confusion possible.
Inutile de passer par √2² : √4 = 2.

La question 2 est identique à la première :
AH²=AC²-HC²
AH² = a² - (a/2)²
Continue le calcul, réduis au même dénominateur.

D'accord, merci

AH²=a²-a²/4
= 4a²/4 - a²/4
= 4a²-a²/4
= 4/4
= 1

Je ne suis pas sûre que ce soit ça

Sans parenthèses, le calcul devient faux. Et où est passée la lettre a ?
AH² = 4a²/4 - a²/4
= (4a² - a²)/4
= ?? la soustraction n'est pas une "suppression" ! les a² ne s'en vont pas.
Imagine : (4 trucs - 1 truc) cela donne quoi ?

Aah oui pardon !

HA²= (4a²-a²)/4
= 3a²/4

Oui.
Il n'y a plus qu'à prendre la racine carrée de tout cela.

D'accord
HA =( √3a²/4)
= √3a²/√4
= √3a²/2
= √(3 × a²)/2
= √3 × √a²/2
= a√3/2

Oui, mais dès la seconde ligne, il faut mettre des parenthèses :
√(3a²)/√4
Tu remarques ce que je t'ai déjà dit dans un autre sujet : le nombre √3 intervient dans les triangles équilatéraux.
Le résultat final peut s'énoncer ainsi :
pour obtenir la hauteur d'un triangle équilatéral, on multiplie la longueur du côté par le nombre √3, et on divise le résultat par 2 (à retenir).

D'accord je m'en rappellerais. Oui je l'ai remarqué, c'est très subtil. Merci pour votre aide en tout cas ! Au revoir.

De rien.
A plus tard.