Fonction Domaine de définition
-
Sserenade dernière édition par
Bonjour
Je veux que l'on me corrige ces exercices s'il vous plaît
Mercif(x) = (x+4)(x−1)(x−7)(3−x)\frac{(x+4)(x-1)}{(x-7)(3-x)}(x−7)(3−x)(x+4)(x−1)
g(x) = 4x2+3x−4\frac{4}{x^2+3x-4}x2+3x−44
h(x) = x12−2x2\frac{x}{12-2x^2}12−2x2x
m(x) = (x+4)(x−1)(x−7)(3−x)\frac{\sqrt{(x+4)(x-1)}}{(x-7)(3-x)}(x−7)(3−x)(x+4)(x−1)
n(x) = −x2+3x+1\sqrt{-x^2+3x+1}−x2+3x+1
p(x) = 1−x+xx2−9\sqrt{1-x} + \frac{x}{x^2-9}1−x+x2−9x
Résultats
Df = R{7;3}Dg = R{-4;1}
Dh = R
Dm = R{0;6}
Dn = R](3-V13)/2U/2[
Dp = je bloque
-
mtschoon dernière édition par

Bonjour,
Idées :
on ne peut pas diviser par 0
on ne peut pas prendre la racine carrée d'un nombre strictement négatifJe regarde tes réponses;
Oui pour Df et Dg
Pour Dh : à revoir.
il faut imposer la condition :
12−2x2≠012-2x^2 \ne 012−2x2=0
Pour Dm : à revoir.
il faut imposer les conditions :
$\left{(x+4)(x-1) \ge 0\(x-7)(3-x) \ne 0\right$
Pour Dn : à revoir ( pas clair)
Dn=[3−132,3+132]D_n=[\frac{3-\sqrt{13}}{2},\frac{3+\sqrt{13}}{2}]Dn=[23−13,23+13]
Pour Dp : à revoir.
il faut imposer les conditions :
$\left{1-x \ge 0\x^2-9 \ne 0\right$
-
VVenx dernière édition par
Bonjour,
Df est correctDg aussi mais on aurait tendance à écrire R{1;-4} mais je chipotte
Tu as erreur sur le Dh, est tu sur que tu as aucune annulation de ton dénominateur (regarde pour les racines de 12 par exemple)
Le Dm n'est pas correct, tu as deux conditions à respecter, l'intervalle pour ta fonction racine carré, et les valeurs interdites de ton dénominateur, ton Dm sera l'intersection des 2.
Ta notation de Dn n'est pas correct, tu dois certainement vouloir dire R](3-V13)/2;(3+V13)/2[, dans ce cas ce n'est pas correct, si tu voulais dire
R]-inf;(3-V13)/2'U'/2;+inf[ c'est bon mais dans ce cas préfère la notation Dn=[(3-V13)/2;(3+V13)/2]Pour le Dp regarde quand est défini ta racine, puis quand est définie ton rapport, et tu fais l'intersection des deux sa devrait marché.
Sinon tu transforme ta relation en rapport et tu regarde le domaine de définition mais ça revient au mêmeModif:Oups, je rédigeais en même temps que toi désolée mtschoon
-
mtschoon dernière édition par

Bonjour Vens.
Aucune importance !
-
Sserenade dernière édition par
Merci de vos réponses
Voilà ce que j'ai reprisPour h(x) sur le dénominateur c'est 12+2x^2
Pour Dm
(x+4)(x-1) ≥ 0
(x-7)(3-x) ≠ 0Dm = R{{-3;7}U[-4;1]} pas vraiment sûre de moi
Dn = ]-oo;(3-V13)/2U/2;+oo[
Dp = R{]-oo;1]U{-3;3}} pas sûre
-
Sserenade dernière édition par
Dans le cas de m(x) j'ai
au numérateur Dm donne ]-oo;-4]U[1;+oo[
et au dénominateur j'ai x≠-3 et x≠7Comment trouver le domaine de définition de m(x) s'il vous plaît
-
VVenx dernière édition par
Ok pour le h(x) si tu as un +
Pour m(x)
Tu as tes 2 conditions x doit appartenir à ton premier intervalle mais il ne doit pas prendre 2 valeurs, donc tu exclus de ton intervalle les deux valeurs,
Est-ce que 3 est dans ton intervalle ? Oui ou non ai-je besoin de l'exclure ?
Est-ce que 7 est dans ton intervalle ? Oui ou non ai-je besoin de l'exclure ?
Tu as le droit d'écrire si c est entre a et b Dm=[a;c[U]c;b]
Toi ce que tu as écris c'est que tu écris c'est que tu colles les intervalles suivant :-3..7; -inf ..-4 et 1 .. +inf tu ne peux pas il se recoupe sa ne veut donc rien dire. Pour t'aider vois les intervalles comme des distance sur une règle, regarde si dessous c'est absurde de réunir mes 2 intervalles.: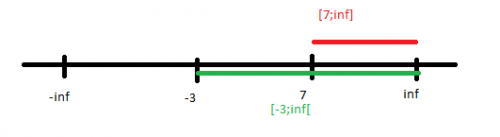
Pour Dp
Tu as les valeurs mais ta notation n'est pas bonne, le A{b} signifie que tu prend l'intervalle A et tu lui enlève juste la valeur b.
Toi là tu prend l'intervalle de tous les réels et tu lui enlève un intervalle et 2 valeurs.
Regarde simplement pour quelle valeur ma fonction est correct. Un peu comme pour le Dn et pareil pour enlever les valeur regarde le Dm
-
Sserenade dernière édition par
Merci je viens de voir mon erreur sur Dn excusez moi
c'est bien Dn =[(3-V13)/2;(3+V13)/2]
-
mtschoon dernière édition par zipang

Pour h(x), tu avais écrit, pour le dénominateur 12-2x²
S'il y avait une faute de frappe, est si le dénominateur est 12+2x² , Dh=R
Attention : Pour m(x), le dénominateur s'annule pour
3et 7 ( au lieu de -3 et 7)Pour mieux comprendre les intervalles, tu peux placer les valeurs sur un axe (et supprimer ce qui ne convient pas)
Tu peux écrire :
Dm=]−∞,−4]∪[1,3[∪]3,7[∪]7,+∞[D_m = \left]-\infty ,-4\right] \cup \left[1,3 \right[ \cup \left]3, 7 \right[ \cup \left]7, +\infty \right[Dm=]−∞,−4]∪[1,3[∪]3,7[∪]7,+∞[
-
Sserenade dernière édition par
Merci encore une fois de plus à Venx et à mtschoon
Mais j'ai une question pour m(x) est ce que si je faisais un tableau de signe est ce que je mettrais les valeurs qui annule le dénominateur de m(x)
-
VVenx dernière édition par
Si tu fais un tableau de signe et que ces valeurs sont dans ton intervalle principale, tu les signale en faisant une double barre sur ton tableau de signe (sa signifie non définie). Ce qui en gros dit que tu peux avoir un saut de valeur (passer de -inf à +inf)
Si on prend la fonction 1/x qui est définie sur R{0} on aurait le tableau de variation (pas de signe dsl) suivant :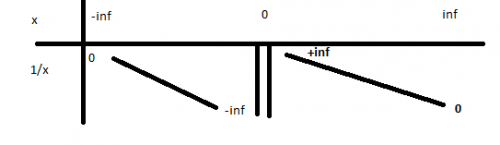
-
Sserenade dernière édition par
Merci Venx est ce que vous pourriez me faire le tableau de signe de m(x) si c'est possible même si c'est demain s'il vous plaît afin que je puisse avoir un aperçu?
-
VVenx dernière édition par
Fais le pour t’entraîner on te corrigera, au passage j'ai fais un tableau de variation pas de signe mais il repose sur le même principe.
Pour Dm tu fais la double barre en 3 et 7 et tu laisse l'espace entre -4 et 1 vide. (Désolée mais j'avais déjà ce tableau de variation sur mon pc et je trouvais qu'il illustrait les discontinuités mais ne t'embrouille pas avec ça)
-
Sserenade dernière édition par
j'essaierai de poster un tableau demain je le ferai sous word pour voir
Merci de votre aide
-
mtschoon dernière édition par zipang

Si ça t'arrange, voici le tableau de signes du produit (x+4)(x-1) sur R
$\begin{tabular} {|c|ccccccccccccc|}\hline x&-\infty&&&-4&&&&1&&&&&+\infty\ \hline (x+4)&&-&&(0)&&+&&(5)&&&+\ (x-1)&&-&&(-5)&&-&&(0)&&&+\ \hline (x+4)(x-1) &&+&&(0)&&-&&(0)&&&+\ \hline \end{tabular}$
Tu aurais pu aussi développer (x+4)(x-1) qui t'aurait donné un polynôme du second degré dont tu aurais pu trouver le signe
La condition(x+4)(x−1)≥0(x+4)(x-1) \ge 0(x+4)(x−1)≥0 est réalisée pour x∈]−∞,−4]∪[1,+∞[x \in ]-\infty,-4] \cup [1,+\infty[x∈]−∞,−4]∪[1,+∞[
A cet ensemble, il faut supprimer les valeurs 3 et 7 qui annulent le dénominateur.
Donc Dm=(]−∞,−4]∪[1,+∞[)/3,7D_m=( ]-\infty,-4] \cup [1,+\infty[ ) / {3,7}Dm=(]−∞,−4]∪[1,+∞[)/3,7
Tu peux représenter les valeurs sur un axe et écrire Dm sous forme de l'union de quatre intervalles, comme je te l'ai indiqué précédemment.
Regarde le schéma : D_{m }$est en vert(et les valeurs "interdites" sont en
rouge).
-
Sserenade dernière édition par zipang
Merci infiniment Mtschoon je comprends beaucoup mieux grâce à ton aide et à celle de Venx
-
mtschoon dernière édition par

C'est parfait si maintenant tu as bien compris DmD_mDm
Demande si DpD_pDp n'est pas clair pour toi.
-
Sserenade dernière édition par
J'ai essayé de résoudre Dp voici mon résultat
pour Dp
1-x ≥ 0
x^2 - 9 ≠ 0x ≤ 1 et x≠ 3 et x ≠ -3
Dp = ]-oo;-3[U]-3;1]si c'est bon est ce que je pouvais écrire tout simplement ]-oo;1]
-
mtschoon dernière édition par zipang

Ta première écriture de DpD_pDp est bonne ( bravo ! )
Si tu veux écrire DpD_pDp en utilisant ]-∞ ; 1] , à cet intervalle, il faut ôter -3
Tu peux donc aussi écrire :
Dp=]−∞,1]/−3D_p=]-\infty , 1] / {-3}Dp=]−∞,1]/−3
-
Sserenade dernière édition par
Merci
-
mtschoon dernière édition par

De rien!
A+