Exprimer la probabilité p d'obtenir un jeton n°2 au nième tirage
-
Bbrom2 dernière édition par Hind
Bonjour, je ne parviens pas à faire cet exercice de probabilités:
On dispose de 2 sacs contenant respectivement: pour le sac n°1: 4 jetons n°1 et 6 jetons n°2 et pour le sac n°2: 6 jetons n°1 et 4 jetons n°2. On tire un premier jeton dans le sac n°1 (tirage avec remise), on continue ensuite des tirages suivant le protocole suivant, le sac dans lequel s'effectue le tirage avec remise d'un jeton est celui ayant le même numéro que le jeton tiré lors du tirage précédent. Exprimer en fonction de n, pour tout n de N*, la probabilité pnp_npn d'obtenir un jeton n°2 au nième tirage.
J'ai fait :
Card (E)=2n(E)=2^n(E)=2n
j'ai ensuite testé lors de plusieurs tirages :- tirer un 2 lors du premier tirage :
p1p_1p1=(6C1 + 4C1)/2
p2p_2p2=(4C16C1)+(6C16C1)/4
merci de m'aider
- tirer un 2 lors du premier tirage :
-
mtschoon dernière édition par

Bonjour,
Je ne comprends guère le début de ta démarche.
Piste de travail ,
Je te suggère de faire des arbres probabilistes, car des petits schémas éclairent les raisonnements.
De façon simple, tu peux prouver que :
le sac 1 étant choisi, la probabilité de tirer 1 est 4/10=0.4 et la probabilité de tirer 2 est 6/10=0.6
le sac 2 étant choisi, la probabilité de tirer 1 est 6/10=0.6 et la probabilité de tirer 2 est 4/10=0.4
Tu peux chercher une relation de récurrence entre pnp_{n }pnet pn+1p_{n+1}pn+1
Principe :
p1p_1p1=0.6
Soit pnp_npn la probabilité de tirer 2 au nieˋmen^{ième}nieˋme tirage
La probalilité de tirer 1 au nieˋmen^{ième}nieˋme tirage est donc 1−pn1-p_n1−pnJe te mets l'arbre (correspondant au niemen^{ieme}nieme et (n+1) iemei^{eme}ieme tirages)
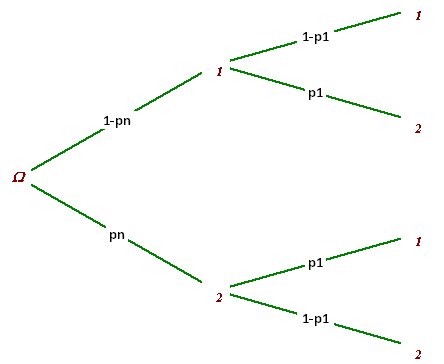
Tu peux déduire :
pn+1=(1−pn)p1+(pn)(1−p1)p_{n+1}=(1-p_n)p_1+(p_n)(1-p_1)pn+1=(1−pn)p1+(pn)(1−p1)
Tu transformes, tu remplaces p1p_1p1 par sa valeur et tu trouves une relation de la forme
pn+1=apn+bp_{n+1}=ap_n+bpn+1=apn+b
Tu étudies cette suite et tu trouves l'expression de pnp_npn en fonction de n
-
Bbrom2 dernière édition par
donc :
pn+1p_{n+1}pn+1=0.6(1−p6(1-p6(1−p_n)+pn)+p_n)+pn*0.4
donc pn+1p_{n+1}pn+1=0.6-0.6pn6p_n6pn+0.4pn4p_n4pn
pn+1p_{n+1}pn+1=0.6-0.2pn2p_n2pndonc pnp_npn=-0.2n−12^{n-1}2n−1*0.1 (à vérifier je pense avoir fait une erreur mais je veux juste le principe)
et une fois cela fait que faire ensuite ?
-
mtschoon dernière édition par

Cela me semble bien être
pn+1=−0.2pn+0.6p_{n+1}=-0.2p_n+0.6pn+1=−0.2pn+0.6
cette relation s'appelle relation de récurrence affine d'ordre 1
On peut dire que la suite (pn(p_n(pn) est "arithmético-géométrique"
Regarde si tu trouves cela dans ton cours.
l'expression de pnp_npn que tu donnes est très bizarre.
Pour la méthode, si ton cours ne t'éclaire pas, tu peux regarder ici :
-
Bbrom2 dernière édition par
oui j'ai du faire une erreur de calcul. Je retrouverai le bon résultat sur papier car je serai plus à l'aise.
Une fois que j'ai la formule, comment répondre à la question posée?
-
mtschoon dernière édition par

L'énoncé indique :
Citation
Exprimer en fonction de n, pour tout n de N*, la probabilité pn d'obtenir un jeton n°2 au nième tirageJe ne sais pas trop de quelle formule tu parles...
Si tu as la bonne expression de pnp_npn en fonction de n, tu n'as plus rien à faire.
-
Bbrom2 dernière édition par
d'accord je vais la calculer je croyais qu'il fallait faire autre chose
-
Bbrom2 dernière édition par
j'ai refais mes calculs et au final je trouve :
voici les détails :vvvn=pn=p_n=pn-0.5
vvv{n+1}=pn+1=p_{n+1}=pn+1-0.5
vn+1v_{n+1}vn+1=-0.2pn2p_n2pn+0.1
vn+1v_{n+1}vn+1=-0.2(pn2(p_n2(pn-0.5)Donc vn+1v_{n+1}vn+1=-0.2pn2p_n2pn donc vnv_nvn=-0.2n−12^{n-1}2n−1(0.1) et pnp_npn=-0.2n−12^{n-1}2n−1(0.1) +0.5
-
mtschoon dernière édition par

Je pense que yu as fait une faute de frappe à la dernière ligne.
Citation
vn+1=-0.2pnC'est vn+1=−0.2vnv_{n+1}=-0.2v_nvn+1=−0.2vn
L'expression de pnp_npn me semble bonne, mais mets des parenthèses autour de -0.2, pour éviter toute ambiguité.
pn=(−0.2)n−1(0.1)+0.5p_n=(-0.2)^{n-1}(0.1)+0.5pn=(−0.2)n−1(0.1)+0.5
Avant de recopier ton devoir, vérifie tout depuis le début pour être sûr que tout est bon.