Etude sur les fonctions

Bonjour

C''est exercice je l'ai vu quelque part et j'étais entrain de le traiter mais je bloque à partir de là:
Citation
Que peut-on en conclure pour C et la droite $Δ\Delta$ d'équation y=x-1 ?
Etudier la position de C par rapport à $Δ\Delta$ .

Etudier les variations de f. Tracer C.
Montrer que le point I(-1 ; -2) est centre de symétrie de C

EXERCICE 3
Etude d'une fraction rationnelle
Soit f la fonction définie sur $\mathbb{R} - \lbrace -1 \rbrace par f(x) = \dfrac{x^2+3}{x+1}$ .
On désigne par C la courbe représentative de f dans le plan rapporté au repère orthonormal $\vec{i} , \vec{j})$ .

Déterminer trois réels a, b et c tels que : pour tout $\in D , , , f(x) = a x + b + \dfrac{c}{x + 1}$ .
Etudier les limites en $+∞+\infty$ et $−∞-\infty$ de la fonction g définie sur D par : g(x) = f(x) - x + 1.
Que peut-on en conclure pour C et la droite $Δ\Delta$ d'équation y=x-1 ?
Etudier la position de C par rapport à $Δ\Delta$ .
Etudier les variations de f. Tracer C.
Montrer que le point I(-1 ; -2) est centre de symétrie de C

Merci de m'aider à comprendre cette partie et surtout comment faire ce tableau de variation?

Bonjour,

(Ici, tu peux mettre des images contenant exclusivement des graphiques sans texte)

Je suppose que tu as trouvé

$f(x)=x−1+4x+1f(x)=x-1+\frac{4}{x+1}$

Lorsque x tend vers +∞ ou -∞, 4/(x+1) tend vers 0, donc la courbe d'équation y=f(x) "s'approche" indéfiniment de la droite d'équation y=x-1

Cette droite est donc asymptote à la courbe.

$g(x)=f(x)−(x−1)=4x+1g(x)=f(x)-(x-1)=\frac{4}{x+1}$

Pour la position de la courbe par rapport à l'asymptote, tu dois étudier le signe de g(x)

Lorsque g(x)>0, f(x)-(x-1) > 0, f(x) > (x-1) : (C) au dessus de (Δ)
Lorsque g(x)<0, f(x)-(x-1) < 0, f(x) < (x-1) : (C) en dessous de (Δ)
Lorsque g(x)=0, f(x)-(x-1) = 0, f(x) = (x-1) : (C) coupe (Δ)

Pour t'expliquer le tableau de variation, il faut que tu nous donnes la dérivée que tu as trouvée ( car le tableau de variation dépend du signe de f'(x) )

Merci mtschoon

j'ai bon sur les résultats que tu as donné là...
pour f'(x) = 1 - (4 / (x+1)²)

Je te suggère de réduire au même dénominateur :

$\fbox{f'(x)=\frac{(x+1)^2-4}{(x+1)^2}}$

Sur R/{-1}, $(x+1)2>0(x+1)^2 \gt 0$

f'(x) est doncdu signe du numérateur.

Pour trouver ce signe, tu as le choix.

1ère méthode :

Le plus simple est de factoriser le numérateur avec l'identité remarquable
a²-b²=(a+b)(a-b)

$x+1)^2-4=(x+1)^2-2^2=(x+1+2)(x+1-2)=(x+3)(x-1)$

Tu fais un tableau de signe pour avoir le signe de ce produit sur R :

$\begin{tabular} {c|cccc} x&-\infty&&&-3&&&&1&&&&&+\infty&\ \hline (x+3)&&-&&(0)&&+&&(4)&&&-\ (x-1)&&-&&(-4)&&-&&(0)&&&+\ \hline (x+3)(x-1)&&+&&(0)&&-&&(0)&&&+ \end{tabular} \$

Pour le tableau de variation, il faut penser, en plus, à mettre une double barre à -1 valeur "interdite")

2ème méthode ( plus lourde )

Tu développes le numérateur

$x+1)^2-4=x^2+2x+1-4=x^2+2x-3$

Tu cherches les valeurs qui annulent ce poynôme et son signe ( polynôme du second degré )

Rebonjour

Donc pour le signe du numérateur on a:
f(x) > 0 pour x ∈ ]-oo;3]U[1;+oo[
f(x) < 0 pour x ∈ [-3;1]

Attention : il ne s'agit pas de f(x) mais def'(x) ( la dérivée)

Pour f '(x), il faut aussi supprimer (-1) (à cause du dénominateur)

f '(x) > 0 pour x ∈ ]-∞;-3[U]1;+∞[

f '(x) < 0 pour x ∈ [-3;-1[ U ]-1,1[

f '(x) = 0 pour x=-3 et pour x=1

Merci mais pourquoi les crochets sont-ils ouverts pour -3 et 1
mais -1 ne figure pas dans le tableau

Comme je te l'ai indiqué, pour clarifier, je t'ai donné de signe du produit (x+3)(x-1) sur R

Si tu préfères, tu peux donner le signe du produit (x+3)(x-1) sur R/{-1} en mettant une double barre -1; c'est ce qu'il faudra faire pour le tableau de variation de f car Df=Df'=R/{-1}

Pour -3 et 1, f '(x)=0

Ainsi rédigé , -3 et 1 ne font partie ni du cas f '(x) > 0 , ni du cas f '(x) > 0

Pour que I soit centre de symétrie de C
je fais
x = - 1 + X
y = -2 + Y

je remplace dans f(x)
y - 2 = (-1+x) -- (4 / (-1+x)+1)

est ce bien sa

Je suppose que tu as compris le tableau de variation, vu que tu n'en parles pas.

Pour le centre de symétrie I , ton départ est juste .

$y=-2+Y\fbox{x=-1+X \ y=-2+Y}$

Ensuite, tu dois, tout simplement, remplacer x et y par ces expressions dans : $y=x2+1x+1y=\frac{x^2+1}{x+1}$

Cela de tonne :

$−2+Y=(−1+X)2+3(−1+X)+1-2+Y=\frac{(-1+X)^2+3}{(-1+X)+1}$

$Y=(−1+X)2+3(−1+X)+1+2Y=\frac{(-1+X)^2+3}{(-1+X)+1}+2$

En transformant le membre de droite, tu dois arriver à :

$\fbox{Y=\frac{X^2+4}{X}}$

Soit g cette fonction définie par : $Y=g(X)=X2+4XY=g(X)=\frac{X^2+4}{X}$

En démontrant que g est impaire ( car g(-X)=-g(X) ), tu déduis queI est centre de symétrie.

Bonjour mtschoon
le tableau de variation m'intéresse beaucoup mais je n'arrive pas a le faire et j'ai vraiment besoin qu'on me l'explique

Principe pour le tableau de variations, (je suppose que tu l'as vu en cours)

Une ligne pour x (avec les valeurs -3,-1,1)

(mets une double-barre verticale à -1)
Une ligne pour f '(x) avec les signes trouvés précédemment
Une ligne pour f avec flèches (* flèche montant quand f '(x) > 0 et flèche descendante quand f '(x) < 0*)

Tu complètes avec les limites ( si tu les as calculées) et avec les valeurs f(-3)=-6 et f(1)=2

g(x) = (x²+4) / x
déterminons g(-x)

g(-x) = ((-x)² + 4) / (-x) = - ((x²+4) / x)

on constate que g(x) = - g(x)
alors g(x) est impair
Par conséquent I est centre de symétrie de la courbe C.

je reprendrai le tableau et je posterai mais y a des choses que je ne comprends pas encore sur le tableau lorsque vous dites
Citation
Tu complètes avec les limites ( si tu les as calculées)

bonne soirée mtschoon

Dans un tableau de variation, il est parfois demandé (par le professeur) seulement les "variations", c'est à dire les flèches et extrema.

Bien sûr, si les limites aux bornes de l'ensemble de définition sont déjà faites, on les met .

bonjour

ici les limites sont a linfini, mais est ce qu'on a besoin de faire le graphique dabord avant de faire le tableau de variation

"les limites sont à l'infini" ne veut pas dire grand'chose...

ici :

$f(x)=−∞\lim_{x\to -\infty}\ f(x)=-\infty$

$f(x)=+∞\lim_{x\to +\infty}\ f(x)=+\infty$

$f(x)=−∞\lim_{x\to( -1)^- }\ f(x)=-\infty$

$f(x)=−∞\lim_{x\to( -1)^+}\ f(x)=-\infty$

Le sens de variation est la conséquence directe du
signe de la dérivée.

La représentation graphique se fait après.

Evidemment, elle peut te servir de vérification, mais ce n'est pas un outil de démonstration.

merci pour tes explications. Pourquoi faut-il determiner lim de (-1)

Comme j te l'ai déjà indiqué, dans un tableau de variation, les limites ne sont pas imposées.

-1 est la valeur interdite. f(-1) n'existe pas.
Il est donc légitime de se demander ce que fait f(x) lorsque x s'approche de -1 ( par valeurs inférieures à -1 , et par valeurs supérieures à -1 )

Si ça t'est utile, je te mets le tableau de variation complet (avec les limites)

(Il n'est pas génial car en Latex ce n'est pas commode, alors je l'ai construit avec Geogebra...)

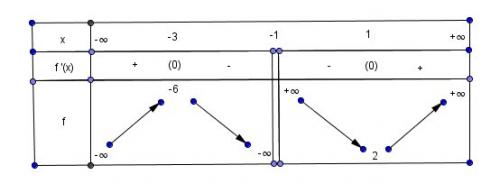
$fichier math$

cela m'aide beaucoup comme ça

mais comment lit-on "mathématiquement" ce tableau
les flèches je veux dire de -oo à -6 de -6 à -oo et ensuite +oo à 2 et 2 à +oo?

Et ce sera ma dernière question
Merci très sincèrement

Mais..., tu n'a pas de cours ?

flèche montante : fonction croissante
flèche descendante : fonction décroissante

Jai pas compris votre question mais s'il s'agit des cours à l'école aujourd'hui jai pas cours mais à cause des débrayages il arrive qu'on ait pas cours

je fais la serie L2 mes matières dominantes sont la philo, le français et l'histo-geo mais comme je suis nulle en math quand j'ai pas cours je me connecte pour faire mes devoirs et parfois je traite quelques exercices que je trouve dans le net.

Merci de ton aide mtschoon
Bonne soirée

Je m'étonnais que dans ton cours de maths, il n'y ait pas d'explications sur les "flèches", mais merci pour tes indications sur ta série.

"Nulle en maths" ? pourquoi donc. Il n'y a aucune raison.
En travaillant , tu vas progresser.

Bon courage et bonne soirée.