Pavé droit, aire
-
RRaissat069 dernière édition par
Bonjour, je n'arrive pas à résoudre cette exercice, pouvez vous m'aider svp ?
Toutes les longueurs sont en centimètres ABCDEFGH est un pavé droit.
AEGC est un rectangle de centre O, avec OE = √6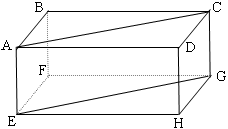
Légendes n'étant pas sur la figure : EH=√5, GC=√3
Les diagonales de AEGC se coupent en un point O1/ Calculez l'aire exacte du rectangle AEGC.
2/Justifiez que la longueur HG est un nombre entier.
-
mtschoon dernière édition par

Bonjour,
Piste,
AEGC est un rectangle.
aire(AEGC)=EG x GC
GC=√3
Il reste à calculer EG
Pour cela, utilise le théorème de Pythagore dans le triangle rectangle EGC
EG²+GC²=EC²
GC²=3
EG=2OE=2 √6
donc EG²=4 x 6 = 24
24=EG²+3
Tu peux ainsi déterminer EG² puis EG puis l'aire du rectangle AEGC.
-
RRaissat069 dernière édition par
Ah d'accord, donc...
EC²=GC²+EG²
EG²= EC²-GC²
= 24 - (√3)²
= 24 - 3
= 21
EG = √21Aire (AEGC) = √3 × √21
= √3 × √7×√3
=(√3)² × √7
= 3√7
L'aire de AEGC est de 3√7 cm²C'est ça ?
-
mtschoon dernière édition par

C'est bon.
Maintenant, il te reste à calculer HG
(je te conseille le théorème de Pythagore dans le triangle EHG)
-
RRaissat069 dernière édition par
Dans HEG rectangle en H, j'applique Pythagore et j'ai
EG²=HG²+EH²
HG²= EG²-EH²
=(√21)²-(√5)²
= 21 - 5
= 16
HG = √16
= 4
Dong HG est bien un nombre entier
-
mtschoon dernière édition par

C'est tout à fait exact.
-
RRaissat069 dernière édition par
 Merci pour votre aide, c'était en fait vraiment facile... La prochaine fois je réfléchirai plus longtemps !
Merci pour votre aide, c'était en fait vraiment facile... La prochaine fois je réfléchirai plus longtemps !
-
mtschoon dernière édition par

De rien et bonne initiative ; toute réflexion est utile!